| Autor |
Beitrag |
    
Philip Meyer zu Spradow (Drmac)

| | Veröffentlicht am Montag, den 05. März, 2001 - 10:13: | 
|
f t (x) = (tx^2-4) / (x^2), t e R+
Leider weiß ich nicht wie man folgende Aufgabe löst :
Für welchen Wert t berührt eine Parabel p(x)=ax^2+c mit dem Scheitelpunkt (0/-1)den Graphen f t in seinen Nullstellen ? |
    
Fern

| | Veröffentlicht am Montag, den 05. März, 2001 - 12:27: | 
|
Hallo Philip,
f(x)= (tx² - 4)/x²
p(x) = ax² + c
============
Scheitel von p(x) liegt bei (0; c) aber auch bei (0;-1)
daher c = -1
p(x) = ax² - 1
=========
Nullstellen von f(x):
tx²-4 = 0
x = ± 2/W(t)
===============
Wir bilden Ableitungen:
f'(x) = 8/x³
p'(x) = 2ax
===========
Wir untersuchen zunächst die Nulstelle x = + 2/W(t)
p(2/W(t)) = 4a/t - 1
p'(2/W(t)) = 4a/W(t)
f(2/W(t)) = 0
f'(2/W(t) = t3/2
====================
Es gelten folgende Bedingungen:
p(2/W(t)) = f(2/W(t))
p'(2/W(t)) = f'(2/W(t))
also:
4a/t -1 = 0
4a/W(t) = t3/2
==============
Aus diesen beiden Gleichungn: t = 1 und a = 1/4
====================
Für diese Werte wid:
f(x) = (x² - 4)/x²
p(x) = x²/4 - 1
=============
Für den 2. Wert für x, ergibt sich das gleiche Resultat.
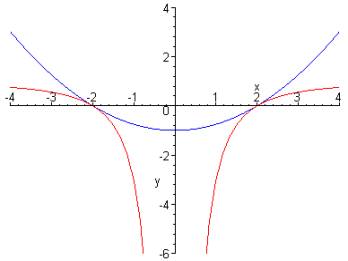 |
|