| Autor |
Beitrag |
    
Marius (Neo_Greek)

| | Veröffentlicht am Donnerstag, den 01. März, 2001 - 16:35: | 
|
Hallo!
Wie lautet die ELIPSENGLEICHUNG?
Wie berechnet man damit das Volumen eines Fasses?
gegeben:
Höhe des Fasses (6dm)
Durchmesser in der Mitte (4dm)
Durchmesser der Grund- und Deckfläche (7^(1/2)dm "Wurzel 7")
Danke |
    
zechei

| | Veröffentlicht am Donnerstag, den 01. März, 2001 - 19:21: | 
|
Die Ellipsengleichung lautet:
in Parameterdarstellung:
x=a*sin w
y=b*cos w
Das Volumen rechnet man mittels Integral und
der Formel für den Rauminhalt eines Drehkegels.
V= phi integral y^2 xpunkt dt
ich hoffe du erkennst die Formel:
xpunkt ist die erste Ableitung von x
viel Spaß
flo |
    
Marius (Neo_Greek)

| | Veröffentlicht am Freitag, den 02. März, 2001 - 15:56: | 
|
Danke Flo!
Ich glaube das hilft mir weiter!
mfg Marius |
    
chris

| | Veröffentlicht am Mittwoch, den 07. März, 2001 - 15:54: | 
|
Hi
Ich hab das selbe Problem, verstehe aber nicht, wofür das "w" in der Parameterdarstellung steht. Wie kann man eine Elipse zeichnen, die durch zwei bekannte Punkte geht. Einer der Punkte soll auf der x-Achse liegen (Koordinaten 0/R) der andere soll die Koordinaten (h/r) haben, wobei R größer als r ist und r größer als 0 ist. Gibt es auch die Möglichkeit die Elipsengleichung anders als durch die Parameterdarstellung zu bestimmen??
ciao Chris |
    
Ysanne (Ysanne)

| | Veröffentlicht am Donnerstag, den 08. März, 2001 - 14:15: | 
|
Es gibt noch
x²/a² + y²/b² = 1
Wobei x und y die Koordinaten und a und b die Länge x- bzw. y-Abschnitte sind. a, b sind natürlich größer als 0.
Allerdings hast du Deine Koordinaten gerade falschrum. Normal macht man (x,y) statt (y,x).
Ich dreh also Deine beiden Punkte mal um (h klingt so verdächtig nach Höhe).
Bei Deiner Aufgabe:
(R|0):
R²/a² + 0²/b² = 1
=> a = R
(r|h):
r²/R² + h²/b² = 1
=> b = |Rh|/Ö(R²-r²) |
    
Chris

| | Veröffentlicht am Donnerstag, den 08. März, 2001 - 16:44: | 
|
Vielen Dank für Deine Hilfe. Ich habe jetzt nur noch ein Problem, und zwar wenn ich " r²/R² + h²/b² = 1 " nach " b " auflöse kriege ich immer ein anderes Ergebnis. Was ich jetzt noch brauche sind so'n paar Zwischenschritte bei der letzten Umformung.
ciao Chris |
    
Ysanne (Ysanne)

| | Veröffentlicht am Freitag, den 09. März, 2001 - 10:53: | 
|
Ok. Als Bild dann.
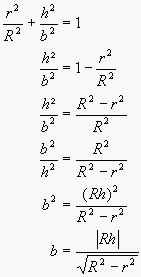
Man beachte, daß der Kehrbruch einer Summe von Brüchen nicht die Summe der Kehrbrüche ist. |
|