| Autor |
Beitrag |
    
dezign

| | Veröffentlicht am Montag, den 22. Januar, 2001 - 20:11: | 
|
Weisen Sie die folgende Rekursionsformel nach.
int. sin^nx dx= -(1/n)*sin^(n-1)x* cosx+ ((n-1)/n)int.sin^n-2x dx
int. = Integral
irgendwie klappt das nicht... ich komme einfach nicht drauf 
erbitte sofortige hilfe 
c´ya |
    
Frank (Norg)

| | Veröffentlicht am Dienstag, den 23. Januar, 2001 - 10:24: | 
|
Das geht mit part. Integration:
òu'v dx = uv - òuv' dx.
òsinnx dx= òsinx * sinn-1x dx = ò(cosx)' * sinn-1x dx.
Den Rest mit der oben beschriebenen Regel.
MfG Frank. |
    
dezign

| | Veröffentlicht am Dienstag, den 23. Januar, 2001 - 18:58: | 
|
thx...
das wußte ich ja schon aber trotzdem danke...
das problem ist , daß es nicht aufgeht... 
wer nimmt erneut anlauf ??? bitte.....
c´ ya |
    
Frank (Norg)

| | Veröffentlicht am Dienstag, den 23. Januar, 2001 - 20:11: | 
|
Bei meinem Ansatz kommt raus:
ò(cosx)'*sinn-1x dx=cosx*sinn-1x-òcosx*(sinn-1x)' dx=
cosx*sinn-1x-òcosx*cosx*(n-1)*sinn-2x dx.
Zur Probe kannst du doch beides einfach mal ableiten:
Du hast geschrieben:
òsinnx dx=
-1/n*sinn-1x*cosx+(n-1)/n*òsin{n-2}x dx
Also muß doch gelten:
sinnx=(-1/n*sinn-1x*cosx+(n-1)/n*òsin{n-2}x dx)'=
(-1/n*sinn-1x*cosx)'+(n-1)/n*sinn-2x=
(-1/n*sinn-1x)'*cosx+(-1/n*sinn-1x)*sinx+(n-1)/n*sin+{n-2}x=
(-1/n*cosx*(n-1)*sinn-2x)*cosx-1/n*sinn+(n-1)/n*sinn-2x=
-1/n*sinn-2x*cos2+(n-1)/n*sinn-2x-1/n*sinnx=
(sinn-2x ausklammern)
sinn-2x*(-1/n*cos2x+(n-1)/n)-1/n*sinnx=
(1/n ausklammern)
1/n*sinn-2x*(-cos2x+n-1)-1/n*sinnx=
(cos2x+sin2x=1 Þ -cos2x-1=sin2x-2)
1/n*sinn-2x*(sin2x-2+n)-1/n*sinnx=
1/n*sinnx+(n-2)/n*sinn-2x-1/n*sinnx=
(n-2)/n*sinn-2x.
Wenn ich keinen Fehler gemacht habe stimmt also deine Formel nicht. Bitte trotzdem um Prüfung.
MfG Frank.
PS.: Da wird einem ganz schön schwummerig. |
    
Fern

| | Veröffentlicht am Dienstag, den 23. Januar, 2001 - 21:29: | 
|
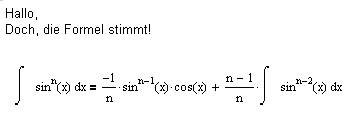 |
    
Frank (Norg)

| | Veröffentlicht am Mittwoch, den 24. Januar, 2001 - 11:31: | 
|
Und? |
    
Fern

| | Veröffentlicht am Mittwoch, den 24. Januar, 2001 - 13:07: | 
|
Hallo dezign und Frank,
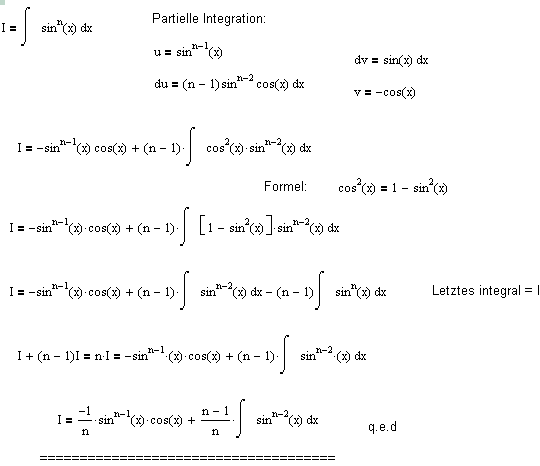 |
    
Stefan (Stefan26)

| | Veröffentlicht am Samstag, den 27. Januar, 2001 - 17:12: | 
|
Hallo Fern,
wie hast Du das tolle Integralzeichen und ie großen Klammern gemacht? |
    
Fern

| | Veröffentlicht am Samstag, den 27. Januar, 2001 - 21:04: | 
|
Hallo Stefan,
Für die Schreibarbeit benütze ich ein Mathematikprogramm namens Mathcad.
Gruß, Fern |
    
Stefan (Stefan26)

| | Veröffentlicht am Samstag, den 24. März, 2001 - 21:05: | 
|
Hallo Fern,
Mathcad kenne ich leider nicht.
Gibt es das auch für UNIX/LINUX?
Gruß,
Stefan |
|