| Autor |
Beitrag |
    
Hubert Wenninger (Matschmotte)

| | Veröffentlicht am Samstag, den 11. November, 2000 - 14:38: | 
|
Lieber "Zahlreich"-Team,
ich stehe vor folgendem Problem:
Wenn bei einer Funktion die erste und zweite Ableitung an einer Stelle 0 sind, handelt es sich um einen Terrassenpunkt. Was aber ist, wenn die dritte Ableitung auch noch 0 ist (die vierte aber nicht)?
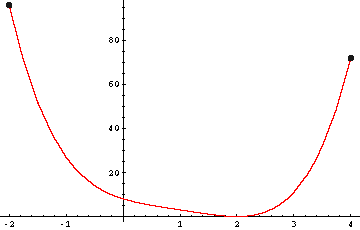
z.B.: f(x)=x^4 bei x=0. Wie nennt man dann den Punkt P(0/0)?
Matschmotte |
    
Ingo

| | Veröffentlicht am Sonntag, den 12. November, 2000 - 03:49: | 
|
Es handelt sich um nichts anderes als einen lokalen Tiefpunkt :-) |
    
Vorsicht

| | Veröffentlicht am Sonntag, den 12. November, 2000 - 23:23: | 
|
 |
    
Geschwafel

| | Veröffentlicht am Sonntag, den 12. November, 2000 - 23:25: | 
|
...den man zusätzlich Flachpunkt nennen kann. Man kann zeigen, dass sich die hinreichende Bedingung für einen Tiefpunkt, f''(x)>0, auf jede geradzahlige Ableitung übertragen kann, also wenn f'(x)=0 =f''(x)=f'''(x) ist und fIV(x)>0 ist, liegt ein TP vor, ebenfalls bei f'(x)=0 =f''(x)=f'''(x)=fIV(x)=fV(x) und fVI(x)>0 usw.
Noch was zum Flachpunkt:
Ein Flachpunkt wiederum muss allerdings kein Tief- oder Hochpunkt sein, sondern kann auch ein Wendepunkt sein (z.B. an der Stelle x=2 der Funktion f(x)=(x-2)5+x; ein Flachpunkt muss noch nicht mal Extremum oder Wendepunkt sein: an der Stelle x=1 bei der Funktion f(x)=(2-x)2(2+x2) liegt ein uneigentlicher Wendepunkt) |
|