| Autor |
Beitrag |
    
Nadice (Nadice)

| | Veröffentlicht am Mittwoch, den 04. Oktober, 2000 - 16:11: | 
|
Hallo kann mir bitte jemand bis heute abend helfen??? WICHTIG!!! (Egal wie spät es wird!)
Also : Funktion f(x)= (x^3+x^2+4) / (2x^2) ; x ungleich 0, mit dem Schaubild K.Graph von f hat an der Stelle x=0 eine senkrechte Asymptote ohne Vorzeichenwechsel; die ersten 3.Ableitungen u.N(-2/0), Extremstellen habe ich : T (2/2), keine Wendepunkte. Jetzt bräuchte ich unbedingt noch die Aufgabe b.) , c.)u.d.)mit Erklärung, damit ich´s auch nachvollziehen kann.Also Aufgabe b.):Die Kurve K, die x-Achse u. die Gerade x=z mit -2<z<0 begrenzen eine Fläche mit Inhalt A(z). Berechne A(z)! Untersuche A(z) für z->0! Hilfe!
Aufgabe c.): Untersuche, ob es eine Parabel mit g(x)= ax^2+bx+c gibt, die das Schaubild sowohl in N(-2/0), als auch in T(2/2) berührt.
Aufgabe d.): Für t>1/2 schneidet die Gerade y=1/2x+t das Schaubilkd K in 2Punkten Pt u. Qt.
Zeige, dass die y-Achse jedes Dreieck 0PtQt in 2 flächengleiche Dreiecke zerlegt.
Ich bitte dringend um Hilfe!!! Komme nicht einen Schritt weiter!!! |
    
Michael (Relaxer)

| | Veröffentlicht am Mittwoch, den 04. Oktober, 2000 - 21:22: | 
|
Hallo Nadice!
Jetzt geb ich diesen ganzen Schlamassel schon zum dritten Mal ein - eine Stunde vollkommen um sonst, es ist zum ...
Aber ich will dir noch schnell wenigstens die Lösung von b) zukommen lassen
A(z)=1/4·z2 + 1/2·z - 2/z - 1
wenn z gegen null geht, dann geht A(z)gegen unendlich
der Rest kommt morgen, bin in Eile!!!
Gruß Relaxer |
    
Nadice (Nadice)

| | Veröffentlicht am Mittwoch, den 04. Oktober, 2000 - 22:36: | 
|
Kannst du mir auch die Rechnung dazu erklären? Ich hab´s mit Integral u. Kepplerscher Faßregel versucht, aber nicht hinbekommen! weiter kam ich dann natürlich erst recht nicht! Leider sollte ich die Aufgabe bis morgen früh um 9.00Uhr haben, bzw. wenigstens kapieren wie es geht.
Ich hoffe das es irgendwie hinhaut, das sich bis dahin jemand meldet der mir helfen kann. |
    
Michael (Relaxer)

| | Veröffentlicht am Donnerstag, den 05. Oktober, 2000 - 06:59: | 
|
Hallo Nadice, gestern abend ging bei mir leider überhaupt nichts mehr aber nun will ich mal ein bisschen Gas geben.
noch mal zu b)
Der Hauptgedanke ist erst mal, dass man aus dem Quotienten eine Summe macht.
f(x)=(x3+x2+4)/(2x2)=x3/2x2+x2/2x2+4/2x2
Man kürzt nun:
f(x)=x/2+1/2+2/x2
Dann lässt sich auch das Integral besser bilden
Int[-2..z](...)dx=1/4·x2+1/2·x-2·x-1[-2..z]
--> A(z)=1/4·z2+1/2·z-2·z-1-1
Aufgabe c) kommt in Kürze!!!
Relaxer |
    
Michael (Relaxer)

| | Veröffentlicht am Donnerstag, den 05. Oktober, 2000 - 07:31: | 
|
weiter zu c)
Grundgedanke ist hier, dass man aus den gegebenen Informationen ein Gleichungssystem bastelt und dieses dann löst.
Die Gleichung g(x)=ax^2+bx+c besitzt die drei Koeffizienten a, b und c, d.h. wir brauchen drei Gleichungen bzw. drei Informationen.
Zwei Infos haben wir schon über die Punkte
N(-2/0) und T(2,2)
Daraus machen wir
(1) a·(-2)^2+b·(-2)+c=0
(2) a·22+b·2+c=2
oder besser
(1) 4a-2b+c=0
(2) 4a+2b+c=2
Die 3. Info kriegen wir aus dem Anstieg
f'(-2)=g'(-2)
f'(x)=1/2-4x-3 also --> f'(-2)=g'(-2)=1
allgemein:
g'(x)=2ax+b
also eingesetzt: 2a·(-2)+b=1
bzw.:
(3) -4a+b=1
Wir stellen nach b um: b=1+4a ... und setzen in die oberen beiden Gleichungen (1) und(2) ein:
Um Zeit zu sparen kürze ich die Sache mal hier ab.
(1) 4a-2·(1+4a)+c=0
(2) 4a+2·(1+4a)+c=2
(1) -4a-2+c=0
(2) 12a+2+c=2 (mit -1 multiplizieren)
(1) -4a-2+c=0
(2) -12a-2-c=-2
----------------
--> -16a-4=-2
a=-1/8
Dann folgt b=1/2 und c=3/2
Die quadratische Funktion heißt: g(x)=-1/8·x^2+1/2·x+3/2
Schneller gings nicht!!!
Gruß Relaxer
PS: d) kommt auch noch!!! |
    
Michael (Relaxer)

| | Veröffentlicht am Donnerstag, den 05. Oktober, 2000 - 08:51: | 
|
Hallo Nadice,
nun kann ich mir wahrscheinlich etwas Zeit lassen, denn die magische Zeit von 9.00 ist bereits überschritten.
zu d)
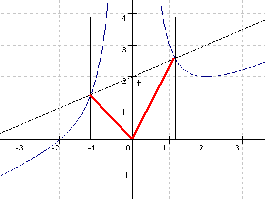
Um d) besser zu verstehen, müsstest du erst mal ne Skizze nach folgender Anleitung anfertigen:
Zeichne zwei parallele Geraden g und h. Lege auf g eine beliebige Strecke AB fest und auf h einen beliebigen Punkt C. Dann haben sämtliche Dreiecke ABC den selben Flächeninhalt, weil die Höhe des Punktes C stets gleich dem Abstand zwischen den Geraden g und h ist. (A=Grundseite·Höhe/2)

Die Grundseite der beiden interessierenden Dreiecke hat die Länge t, also haben die Dreiecke schon mal die selbe Grundseite.
In unserem Beispiel können wir nun durch die Punkte Pt und Qt Parallelen zur y-Achse einzeichnen.
Wenn wir zeigen können, dass diese Senkrechten den selben Abstand zur y-Achse haben, dann ist die Behauptung bewiesen.
Wir berechnen also die Schnittstellen zwischen der Funktion f(x) und der Gerade y=1/2·x+t durch Gleichsetzen.
(x3+x2+4)/(2·x2)=1/2·x+t
x3+x2+4=2·x2·(1/2·x+t)
x3+x2+4=x3+2·x2·t
x2-2·x2·t+4=0
x2·(1-2t)+4=0
x2=-4/(1-2t)
x2=4/(2t-1)
x=+/- sqrt(4/(2t-1))
Über die Schlussfolgerungen brauche ich sicher nichts weiter zu sagen. Damit wäre die Behauptung bewiesen.
Ich hoffe du kommst damit klar, in Zukunft wäre es nicht schlecht, wenn du dich etwas eher melden könntest, denn Stress können wir doch alle nicht vertragen :-)
Gruß Relaxer! |
    
Michael (Relaxer)

| | Veröffentlicht am Donnerstag, den 05. Oktober, 2000 - 08:54: | 
|
 |
    
Nadice (Nadice)

| | Veröffentlicht am Freitag, den 06. Oktober, 2000 - 16:54: | 
|
Relaxer, ich danke dir!!! Habe die Aufgaben am Do. morgen noch durchgecheckt bevor ich zum Unterricht bin. Hat prima geklappt. Jetzt versteh ich wenigstens,was ich da rechne! Gut erklärt!Habe übrigens das gesamte Aufgabenblatt seit So., dem 01.10. in zahlreich.de!!! Du warst nur derjenige, der sie wirklich alle gemacht u. erklärt hat! Danke nochmal, war wirklich dringend. |
|