| Autor |
Beitrag |
    
moin moin

| | Veröffentlicht am Dienstag, den 29. Dezember, 1998 - 14:48: | 
|
Hallo,
eine Frage:
Kann man folgende Aufgabe mit der Regel von l'Hospital lösen, wenn ja - wie, wenn nein - wie dann?
Danke!!
limx->0 (1-cos x)/x² |
    
PimalDaumen

| | Veröffentlicht am Mittwoch, den 30. Dezember, 1998 - 16:30: | 
|
Ja, es geht mit l'Hospital, da Zähler und Nenner für x->0 gegen 0 gehen. Jetzt mußt Du (eben nach l'Hospital) nur Zähler und Nenner ableiten und den Rest so stehen lassen und dann hoffen, daß der neue Limes einfacher zu bestimmen ist - was generell nicht der Fall sein muß. Manchmal hilft auch eine mehrmalige Anwendung der Regel von l'Hospital.
Hier sind die Ableitungen:
Zähler: sin x
Nenner: 2x
was wieder die gleiche Situation "0/0" für x->0 hervorbringt. Also nochmal l'Hospital:
Zähler: cos x
Nenner 2
davon ist der Limes für x->0 offensichtlich ½, was unsere Lösung ist.
Anwenden durften wir die Regel von l'Hospital (welche sicher schon manche Schüler ins Krankenhaus gebracht hat) da Zähler und Nenner jeweils differenzierbar sind und die Ableitung des Nenners jeweils ¹ 0 für x ¹ 0 ist.
Alles klar? |
    
Piet

| | Veröffentlicht am Mittwoch, den 30. Dezember, 1998 - 16:31: | 
|
Sagt mal, wie lautet die Regel von Hospital ?
Danke - Piet |
    
Adam Riese

| | Veröffentlicht am Mittwoch, den 30. Dezember, 1998 - 23:20: | 
|
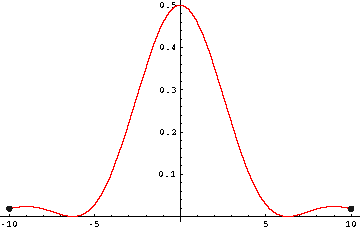
Hallo,
erst mal ein Bildchen zu der Funktion, an der man sich dann das Grenzwertverhalten ganz gut verdeutlichen kann:
f(x) = (1-cos x)/x²
Jetzt Piet zu Deiner Frage. Die Regel von l'Hospital besagt im Wesentlichen, daß
limx->a+ f(x)/g(x) = limx->a+ f'(x)/g'(x)
vorausgesetzt, daß f und g differenzierbar sind auf (a,b) aus R² und g'(x) ohne Nullstellen.
Außerdem ist Voraussetzung, daß |limx->a+ f(x)| = |limx->a+ g(x)| = 0 oder = ¥ gilt.
Kleine Feinheiten habe ich jetzt weggelassen, aber das sollte so genügen.
Noch Fragen?
Grüße - Adam |
    
Cheka

| | Veröffentlicht am Freitag, den 09. Februar, 2001 - 14:53: | 
|
Wie gross sind denn die "kleinen Feinheiten"? |
    
tim

| | Veröffentlicht am Samstag, den 10. Februar, 2001 - 19:19: | 
|
nicht so groß - aber warum fragst Du? |
    
Miri

| | Veröffentlicht am Sonntag, den 25. März, 2001 - 20:47: | 
|
Hallo!
Ich muss ein Referat über Grenzwertbestimmung nach dem Verfahren von l'Hospital schreiben.
Könnt ihr mir helfen?
Danke!!!! :-) |
    
Bärbel Kranz (Fluffy)

| | Veröffentlicht am Montag, den 26. März, 2001 - 07:42: | 
|
Hallo MIri,
hier
http://angelaschule.osnabrueck.de/eigene/schule/facharbeit/famadavi.htm
hab ich was gefunden, was Dich interessieren könnte
Gruss Bärbel |
|