| Autor |
Beitrag |
    
Anonym

| | Veröffentlicht am Dienstag, den 23. Mai, 2000 - 14:55: | 
|
Hallo!
Ich soll bis morgen eine allgemeine Formel zur Berechnung der Mantelfläche(M) eines Kegelstumpfes herleiten.
Mein Problem:Ich kenne die Formel bereits aber ich soll schlieslich den Weg dorthin auch nennen.
Wenn s =Länge einer Mantellinie des Stumpfes, dann soll M=s*pi*(r1+r2) sein! (r=radius)(pi=3,14...)
Wie kommt man zu dieser Formel??? |
    
reinhard (Gismo)

| | Veröffentlicht am Dienstag, den 23. Mai, 2000 - 18:52: | 
|
Hallo!
Vorweg die Skizze
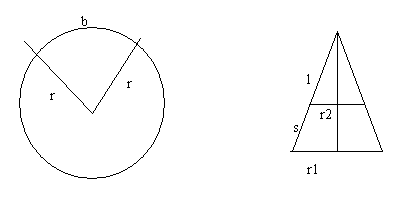
Zulinkerhand siehst du einen Kreis, in dem ein Segment eingezeichnet ist. Wir überlegen nun die Formel für den Flächeninhalt:
Der ganze Kreis hat eine Fläche von r²p. Wir wollen aber nur einen Teil der Fläche. Der Flächeninhalt steht in einem direkten Verhältnis mit der Bogenlänge. Hat ein Segment eines Kreises die doppelte Bogenlänge, so hat es auch die doppelte fläche. Somit hat dieses Segment genau das b/2rp fache des ganzen Kreises, also
A=r²p*b/2rp=rb/2
Um den Mantel des Kegelstumpfes auszurechnen, berechnet man am besten den Mantel des Kegels und zieht dann den Mantel der Kegelspitze ab.
Wenn man am Mantel der Länge nach aufschneidet und aufrollt, erhält man eben solche Kreissegmente, wobei der Radius s+l (l ist die Länge der Mantellinie des Spitzes, der weggeschnitten wird), und die Bogenlänge 2r1p ist. Der Mantel der Spitze bildet auch ein Kreissegment mit dem Radius l und der Bogenlänge 2r2p.
Die Mantelfläche des Kegelstumpfes ist also
A=(s+l)2r1p/2 - l2r2p/2
A=(s+l)r1p-lr2p
Unser Problem liegt nun darin, daß wir das l noch berechnen müssen.
Hierfür betrachten wir die zweite Zeichnung in der Skizze. Der Kegel von der Seite betrachtet sieht so aus. Wir bemerken sofort die ähnlichen Dreiecke:
(l+s):l=r1:r2
(l+s)/l=r1/r2
1+s/l=r1/r2
s/l=r1/r2-r2/r2
s/l=(r1-r2)/r2
l/s=r2/(r1-r2)
l=r2s/(r1-r2)
Nun haben wir l berechnet, welches wir dann in unsere Flächenformel einsetzen können:
A=(s+r2s/(r1-r2))r1p-r2s/(r1-r2)*r2p
=s(1+r2/(r1-r2))pr1 - s(r2/(r1-r2))pr2
=sp[r1/(r1-r2)*r1 - r2/(r1-r2)*r2]
=sp(r12-r22)/(r1-r2)
=sp(r1-r2)(r1+r2)/(r1-r2)
=sp(r1+r2)
Reinhard |
|