| Autor |
Beitrag |
    
Leni (magda1919)

Neues Mitglied
Benutzername: magda1919
Nummer des Beitrags: 5
Registriert: 11-2002
| | Veröffentlicht am Freitag, den 22. November, 2002 - 15:20: | 
|
Hallo,
ich soll die folgende Aufgabe lösen:
Integral (2;5) (x³-9x²+24x+20)dx
Könnt Ihr mir bitte helfen??
Dann soll ich noch die Funktion
f(x)= x³-9x²+24x-20 zeichnen und die funktion
f(x)=-x²+10x-21 mit der Geraden y=1/3x+1
Könnte mir bitte jemand die Zeichnungen an meine E-Mail Adresse schicken? Im Forum sieht man sie ja nicht.Vielen Dank. |
    
Klaus (kläusle)

Erfahrenes Mitglied
Benutzername: kläusle
Nummer des Beitrags: 171
Registriert: 08-2002
| | Veröffentlicht am Freitag, den 22. November, 2002 - 16:00: | 
|
Hallo Leni
Stammfunktion:
F(x) = 0,25x4 - 3x3 + 12x2 + 20x
Nun musst du die Grenzen einsetzen:
A = F(5) - F(2) = 181,125 - 68 = 113,125
---------------------------------------
f(x) geschnitten mit der Geraden y:
-x2 + 10x - 21 = 1/3x + 1
-x2 + 9,66x - 22 = 0
Lösungen dieser quadratischen Gleichungen sind:
x1 = 3 2/3 (3,6666...)
x2 = 6
Schnittpunkt S1 (3/2/3 / 2/2/9)
Schnittpunkt S2 (6 / 3)
MfG Klaus
|
    
Peter (analysist)

Erfahrenes Mitglied
Benutzername: analysist
Nummer des Beitrags: 273
Registriert: 04-2002
| | Veröffentlicht am Freitag, den 22. November, 2002 - 17:31: | 
|
Sieht man doch, oder?
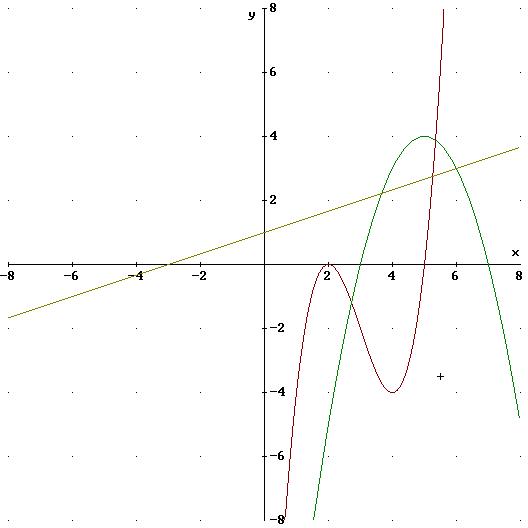
Gruß
Peter |
|