| Autor |
Beitrag |
    
Anonym

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 15:39: | 
|
Ich muß folgende Aufgaben lösen und wäre für deine Hilfe sehr dankbar!
Wie groß ist die Winkelsumme im Dreieck? Beweise deine Behauptung!
Wie groß ist die Winkelsumme in einem beliebigen Viereck? Beweise!
Wie groß ist die Winkelsumme in einem n-Eck? Beweise Deine Behauptung! |
    
reinhard (Gismo)

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 16:15: | 
|
Hallo!
Ich werde die Beweise geometrisch führen:
Behauptung: die Winkelsumme in einem Dreieck ist 180°
Beweis:
Mache durch den Punkt C parallel zur Seite c eine Gerade. Nun kann man die Parallelwinkel von a und b einzeichnen, und man sieht, daß sie zusammen 180° einschließen. Dies gilt für jedes beliebige Dreieck.

Behauptung: Die Winkelsumme in einem Viereck ist 360°
Beweis:
Man teilt einfach das Viereck mit einer Diagonale in zwei Dreiecke, dann ist die Winkelsumme gleich der Winkelsumme der zwei Dreiecke, und wie schon zuvor gezeigt, sind dies je 180°, zusammen also 160°
Behauptung: Die Winkelsumme in einem n-Eck ist (n-2)*180°
Beweis:
Um aus einem Viereck ein Fünfeck zu machen, hängt man an einer Seite des Vierecks ein Dreieck an und hat somit ein Fünfeck. Das heißt, die Winkelsumme eines Fünfeckes ist gleich der Winkelsumme eines Viereckes plus der Winkelsumme eines Dreieckes, also 360°+180°
Um aus einem Fünfeck ein Sechseck zu machen, muß man wieder an einer Seite des Fünfeckes ein Dreieck anhängen, und somit ist die Winkelsumme eines Sechseckes gleich der Winkelsumme eines Fünfeckes plus der Winkelsumme eines Dreieckes, also (360+180)+180
usw....
Die Winkelsumme eines n-Eckes ist gleich der Winkelsumme eines (n-1)Eckes + 180°
Wir machen nun eine kleine Tabelle mit den Winkelsummen:
3-Eck: 180°
4-Eck: 180°+180°°
5-Eck: 180°+180°+180°
6-Eck: 180°+180°+180°+180°
7-Eck: 180°+180°+180°+180°+180°
..
n-Eck: 180°+...+180°=(n-2)*180°

Anmerkung: Die Methode des letzten Beweises, bei der Berechnung eines n-Eckes auf das n-1-Eck zurückzugreifen, nennt man Induktion.
Reinhard |
    
reinhard (Gismo)

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 16:32: | 
|
Entschuldige..wieder mal Probleme mit den Skizzen.
Skizze zum Dreieck:
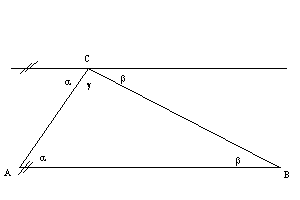
Skizze zum n-Eck:
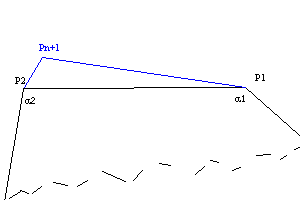 |
    
Anonym

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 18:02: | 
|
Hi Reinhard! Vielen Dank!!! |
|