| Autor |
Beitrag |
    
Chris (mastermail)

Mitglied
Benutzername: mastermail
Nummer des Beitrags: 14
Registriert: 08-2002
| | Veröffentlicht am Sonntag, den 22. September, 2002 - 14:00: | 
|
Hallo,
die Aufgabe lautet:
Bestimmen Sie folgendes unbestimmtes Integral.
ò sin(x)/sin(x)-cos(x)-1 dx
Kann mir bitte jemand erklären wie man das rechnet?
Das Ergebnis allein bringt mir nichts. Ich brauch den Rechenweg aber hab absolut keine Ahnung von der Aufgabe. Vielleicht ist da mit Substitution oder Rekursionsformel was zu machen aber wie geht das ?
Wäre echt super wenn mir da jemand helfen könnte. |
    
Olaf (heavyweight)

Mitglied
Benutzername: heavyweight
Nummer des Beitrags: 47
Registriert: 09-2002
| | Veröffentlicht am Sonntag, den 22. September, 2002 - 14:48: | 
|
Hallo Chris!
Da fehlen doch sicher Klammern,oder?
Gruß,Olaf |
    
egal

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 22. September, 2002 - 15:13: | 
|
Hi Chris,
ò sin(x)/(sin(x)-cos(x)-1) dx =
ò 1 + (cos(x)+1)/(sin(x)-(cos(x)+1)) dx =
ò 1 + 1/(sin(x)/(cos(x)+1) - 1) dx =
ò 1 + 1/(tan(x/2) - 1) dx = [Bronstein Grundintegral]
x/2 + ln(sin(x/2) - cos(x/2))
|
    
Chris (mastermail)

Mitglied
Benutzername: mastermail
Nummer des Beitrags: 15
Registriert: 08-2002
| | Veröffentlicht am Sonntag, den 22. September, 2002 - 17:14: | 
|
Hallo,
mit einer solchen Antwort wie von "egal" hab ich schon gerechnet.
Tolle Rechnung aber leider ohne Erklärung.
Ich hab doch extra dabei geschrieben das ich die
Aufgabe mit Erklärung und Rechenweg haben will.
Wieso macht das keiner ?
Nochmal: Ohne Erklärung bringt mir das NICHTS
Ich hoffe das war jetzt deutlich genug.
Hier nochmal die Aufgabe:
ò sin(x)/(sin(x)-cos(x)-1) dx |
    
Berthold

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 22. September, 2002 - 20:46: | 
|
Hallo Chris,
lern doch zuerst mal Klammern setzen! |
    
Frommhold

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 22. September, 2002 - 22:05: | 
|
Hallo Berthold,
Was stimmt denn nicht mit der Klammersetzung?
ist an
sin(x)/(sin(x)-cos(x)-1)
etwas falsch? |
    
Chris (mastermail)

Mitglied
Benutzername: mastermail
Nummer des Beitrags: 17
Registriert: 08-2002
| | Veröffentlicht am Montag, den 23. September, 2002 - 11:36: | 
|
Hallo,
Frommhold hat da ganz recht, was stimmt mit den
Klammern nicht ?
sin(x) bildet den Zähler.
sin(x)-cos(x)-1 bildet den Nenner.
dx gehört nicht mehr zum Bruch.
Jetzt alles klar ?
Dann bitte eine schnelle klare Antwort.
Gruß Chris
PS: Warum beachtet niemand meinen Beitrag unter
der Linearen Algebra - Rotation um Achsen (die Zweite)? Der steht da schon seit fünf Tagen. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 108
Registriert: 06-2001
| | Veröffentlicht am Montag, den 23. September, 2002 - 16:41: | 
|
Hi Chris,
vieleicht hilft dir dies weiter:
{komLösungsweg}
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 109
Registriert: 06-2001
| | Veröffentlicht am Montag, den 23. September, 2002 - 16:43: | 
|
Hi Chris,
vieleicht hilft dir dies weiter:
{komLösungsweg}
Gruß Niels. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 110
Registriert: 06-2001
| | Veröffentlicht am Montag, den 23. September, 2002 - 16:45: | 
|
Hi Chris,
vieleicht hilft dir dies weiter:

Gruß Niels. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 111
Registriert: 06-2001
| | Veröffentlicht am Montag, den 23. September, 2002 - 16:47: | 
|
Hi Chris,
vieleicht hilft dir dies weiter:

Gruß Niels. |
    
Chris (mastermail)

Mitglied
Benutzername: mastermail
Nummer des Beitrags: 21
Registriert: 08-2002
| | Veröffentlicht am Montag, den 23. September, 2002 - 18:22: | 
|
Hallo Niels !
Vielen Dank, endlich mal jemand der mich erhört.
da ich von dieser Aufgabe aber absolut keine
Ahnung hab, hab ich arge Probleme das zu verstehen
was du da aufgeschrieben hast.
Wie kommst du auf 1+((cos(x)+1)/(sin(x)-cos(x)-1))
kann ich mir nicht erklären.
und der Schritt danach ? Wie geht der ?
Es würde mir sehr weiter helfen wenn du das so
Schritt für Schritt erklären würdest.
1. Schritt..., 2.Schritt... usw.
Sonst zerbrech ich mir noch stundenlang den Kopf darüber. Trotzdem nochmal danke´für die große Mühe. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 112
Registriert: 06-2001
| | Veröffentlicht am Montag, den 23. September, 2002 - 20:25: | 
|
Hi Chris,
schau dir folgendes Buntes Farbenspektakel mal an:
Ich hoffe dann, das du wenigstens die ersten Umformungsschritte verstehst:

Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 113
Registriert: 06-2001
| | Veröffentlicht am Montag, den 23. September, 2002 - 20:27: | 
|
Hi Chris,
schau dir folgendes Buntes Farbenspektakel mal an:
Ich hoffe dann, das du wenigstens die ersten Umformungsschritte verstehst:

Gruß N. |
    
Chris (mastermail)

Mitglied
Benutzername: mastermail
Nummer des Beitrags: 22
Registriert: 08-2002
| | Veröffentlicht am Dienstag, den 24. September, 2002 - 11:26: | 
|
Hi Niels !
Dank deines dokumentierten Lösungsweges hab ich
die meisten Schritten jetzt kapiert.
Nur in der letzten Zeile weiß ich nicht wie
Du zu dem Doppel-Bruch kommst.
Kann es sein das Du gar nicht bis zum Schluß gerechnet hast ?
In dem Beitrag davor hast Du nämlich weiter gerechnet.
Gruß Chris ! |
    
Chris (mastermail)

Mitglied
Benutzername: mastermail
Nummer des Beitrags: 23
Registriert: 08-2002
| | Veröffentlicht am Dienstag, den 24. September, 2002 - 14:32: | 
|
Hi Niels !
Ich hab da noch 'ne andere Aufgabe, die ich jetzt
selber mal versucht habe. Ich komm da aber bei
einem Schritt nicht weiter. Vielleicht kannst Du
mir kurz erläutern wie ich da vorzugehen habe.
Auf dem Aufgabenblatt steht: das die Substititionsregel angewendet werden soll. Ich kenn die aber gar nicht. Geht das so, wie du's
aufgeschrieben hast? Oder ist damit was anderes gemeint ?
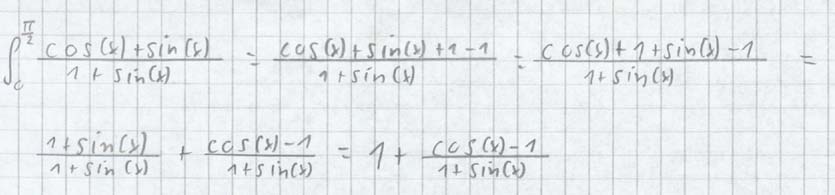 |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 114
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 24. September, 2002 - 14:49: | 
|
Hi Chris,
du hast recht; Ich war gestern Abend noch nicht fertig geworden.
Hier kommt ein weiterer "Umformungsschritt":

und danach müsste man sich noch um das "Bronstein Grundintegral" kümmern...
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 115
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 24. September, 2002 - 14:53: | 
|
Hi Chris,
du hast recht; Ich war gestern Abend noch nicht fertig geworden.
Hier kommt ein weiterer "Umformungsschritt":

und danach müsste man sich noch um das "Bronstein Grundintegral" kümmern...
Hier ein Link dazu:
http://geochron.geologie.univie.ac.at/maths/daten/kap_21/node86.htm
schau dir mal speziell Integral Nr. 416 an!
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 116
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 24. September, 2002 - 14:55: | 
|
Hi Chris,
du hast recht; Ich war gestern Abend noch nicht fertig geworden.
Hier kommt ein weiterer "Umformungsschritt":

und danach müsste man sich noch um das "Bronstein Grundintegral" kümmern...
Hier ein Link dazu:
http://geochron.geologie.univie.ac.at/maths/daten/kap_21/node86.htm
schau dir mal speziell Integral Nr. 416 an!
Gruß Niels. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 118
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 24. September, 2002 - 15:50: | 
|
Hi Chris,
vorab eine Bemerkung:
Ich haben bei der Berechnung deines Integral einen kleinen fehler gemacht:
es müsste als Lösung rauskommen
ò 1/(tan(x/2)-1)dx=-x/2+ln|sin/x/2)-cos(x/2)|
zu deiner anderen Aufgabe:
Lösungsweg prinzipiell richtig:
der Schluß fehlt aber!
Das mit der Substitutionsregel ist keon Problem, allerdings sind deine "Beispiele derart kompliziert, das du mit der Substitutionsregel aleine kein Blumentopf gewinnen kannst. Jedenfalls nicht ohne gleichzeitig die Parzialbruchzerlegung anwenden....
Gruß N.
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 119
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 24. September, 2002 - 22:03: | 
|
Hi Chris,
zum "Bronstein Grundintegral":


mehr dazu Morgen...
Gruß N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 120
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 19:23: | 
|
Hi Chris,
gestern haben wir das "Grundintegrlal" aufgedröselt. Nun müssen wir noch ein bischen die Stammfunktion umformen:

Nun ist Egals Rechnung komplett Nachvollziebar:
wir haben ausführlich gezeigt, das gilt:
ò 1/(tan(x/2)-1)dx=-x/2+ln|sin(x/2)-cos(x/2)|
und
ò 1 + 1/(tan(x/2)-1)dx
=ò 1dx+ò 1/(tan(x/2)-1)dx
=x+(-x/2)+ln|sin(x/2)-cos(x/2)|
=x/2+ln|sin(x/2)-cos(x/2)|
Das Monstrum ist bezwungen!
viele Grüße
N. |
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 121
Registriert: 06-2001
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 19:24: | 
|
Hi Chris,
gestern haben wir das "Grundintegrlal" aufgedröselt. Nun müssen wir noch ein bischen die Stammfunktion umformen:
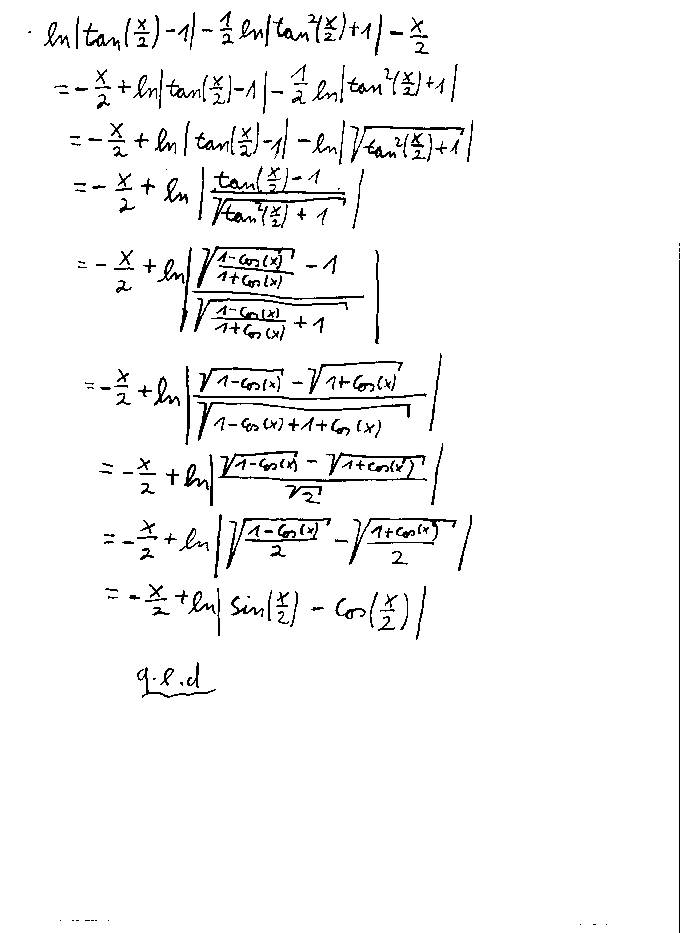
Nun ist Egals Rechnung komplett Nachvollziebar:
wir haben ausführlich gezeigt, das gilt:
ò 1/(tan(x/2)-1)dx=-x/2+ln|sin(x/2)-cos(x/2)|
und
ò 1 + 1/(tan(x/2)-1)dx
=ò 1dx+ò 1/(tan(x/2)-1)dx
=x+(-x/2)+ln|sin(x/2)-cos(x/2)|
=x/2+ln|sin(x/2)-cos(x/2)|
Das Monstrum ist bezwungen!
viele Grüße
Niels |