| Autor |
Beitrag |
    
Bianca Röhl (bianca007)

Neues Mitglied
Benutzername: bianca007
Nummer des Beitrags: 4
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 05. September, 2002 - 18:01: | 
|
Gegeben sind die Funktionen f mit f(x)=e^(0,5x) und g mit g(x)=2*e^-x. Die Graphen von f und g und die x-Achse begrenzen in einem abgeschlossenen Intervall eine Fläche A. Das Intervall hat eine Breite von 2 Längeneinheiten. Bestimmen sie Anfangs- und Endpunkt des Intervalls so, dass der Inhalt der eingeschlossenen Fläche A maximal wird.
Ich habe versucht diese Aufgabe mit x-1; x und x+1 (als Integrationsgrenzen) zu lösen, komme aber nicht wirklich auf eine Lösung. Hat jemand einen besseren Vorschlag? |
    
Peter (analysist)

Mitglied
Benutzername: analysist
Nummer des Beitrags: 30
Registriert: 04-2002
| | Veröffentlicht am Donnerstag, den 05. September, 2002 - 18:57: | 
|
hi,
Wenn beide Funktionsgraphen am Einschließen beteiligt sein soll, muss das Intervall die Schnittstelle enthalten. Diese liegt bei s=2/3ln(2).
Für den Flächeninhalt braucht man dann einmal das Integral von einer stelle s-b bis b über f(x), zum anderen das Integral von s bis s-b+2. Die Funktion in Abhängigkeit von b müsste dann optimiert werden.
Ich komme dann auf eine Funktion
A(b)=-2^(1/3)*e^(b-2)-2*2^(1/3)*e^(-b/2)+3*2^(1/3)
A'(b)=2^(1/3)e^(-b/2)-2^(1/3)e^(b-2)
A''(b)=-2^(1/3)e^(b-2)-(1/2)2^(1/3)e^(-b/2)
aus A'(b)=0 folgt b=4/3
A''(4/3)<0, also lokales Maximum.
Überprüfung der Ränder
A(2)=1,59
A(0)=1,09
A(4/3)=1,84 ist absolutes Maximum
Also muss eine Stelle 4/3 links von der Schnittstelle, die andere 2/3 rechts liegen.
etwas kompliziert, wenn man es "zu fuß" rechnet :-)
Gruß
Peter |
    
Peter (analysist)

Mitglied
Benutzername: analysist
Nummer des Beitrags: 31
Registriert: 04-2002
| | Veröffentlicht am Donnerstag, den 05. September, 2002 - 19:08: | 
|
Sieht aber ganz plausibel aus
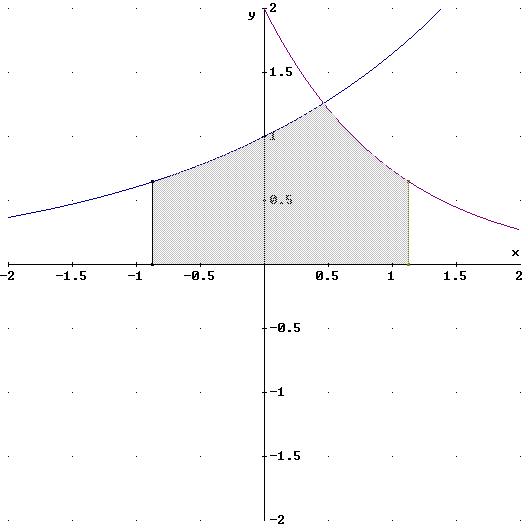
Peter |
    
Bianca Röhl (bianca007)

Junior Mitglied
Benutzername: bianca007
Nummer des Beitrags: 6
Registriert: 03-2002
| | Veröffentlicht am Freitag, den 06. September, 2002 - 18:14: | 
|
Sorry, aber kannst du mir vielleicht nochmal erklären, wie du auf die Gleichung A(b) kommst? |
    
Peter (analysist)

Mitglied
Benutzername: analysist
Nummer des Beitrags: 32
Registriert: 04-2002
| | Veröffentlicht am Montag, den 09. September, 2002 - 14:39: | 
|
Die Funktionen waren: f mit f(x)=e^(0,5x) und g mit g(x)=2*e^-x. Die Schnittstelle hatte ich s genannt.
Die Fläche, die unter dem Graphen von f liegt, lässt sich durch das Integral von s-b bis s berechnen.
Zunächst braucht man eine Stammfunktion zu f,zum Beispiel F(x)=2e^(0,5x).
Die linke Teilffläche ist dann F(s)-F(s-b) groß:
2e^(0,5s)-2e^(0,5s-0,5b)
Jetzt setze ich wieder 2/3ln(2)für s ein:
2*2^(1/3)-2*2^(1/3)e^(-b/2)
---------------------------
Gleiche Prozedur für den rechten Teil
G(x)=-2e^(-x)
G(s-b+2)-G(s)=-2e^(b-s-2)+2e^(-s)
wieder für s eingesetzt:
-2^(1/3)e^(b-2)+2^(1/3)
Beide Terma addiert ergeben A(b).
Gruß
Peter |
|