| Autor |
Beitrag |
    
Tec (technic)

Neues Mitglied
Benutzername: technic
Nummer des Beitrags: 4
Registriert: 08-2002
| | Veröffentlicht am Freitag, den 16. August, 2002 - 16:12: | 
|
Hi
Bei folgenden Integralen blicke ich nicht durch:
Das ganze ist irgendwie speziell...
Ist es nötig, zuerst nur das Integral zu behandeln?
gruss Tec |
    
Tec (technic)

Neues Mitglied
Benutzername: technic
Nummer des Beitrags: 5
Registriert: 08-2002
| | Veröffentlicht am Donnerstag, den 22. August, 2002 - 16:24: | 
|
Ich schnalle immer noch nicht wie ich vorgehen
sollte...
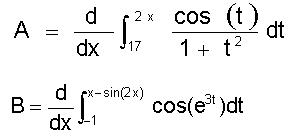
gruss Tec |
    
Christian Schmidt (christian_s)

Erfahrenes Mitglied
Benutzername: christian_s
Nummer des Beitrags: 365
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 22. August, 2002 - 16:48: | 
|
Hi Tec
Das ganze scheint auch nicht so ganz einfach zu sein;) Maple gibt als Lösung für die A folgendes:
-sin(2*x-I)*sinh(1)/(2*x-I)-I*cos(2*x-I)*cosh(1)/(2*x-I)-sin(2*x+I)*sinh(1)/(2*x+I)+I*cos(2*x+I)*cosh(1)/(2*x+I)
Also wärst du da schon im Komplexen:
Bei Aufgabe B:
1/3*cos(e^(3*x)*e^(-3*sin(2*x)))*(3*e^(3*x)*ln(e)*e^(-3*sin(2*x))-6*e^(3*x)*e^(-3*sin(2*x))*cos(2*x)*ln(e))/(e^(3*x)*e^(-3*sin(2*x))*ln(e))
Vielleicht hilft dir das ja weiter...
MfG
C. Schmidt |
    
Tec (technic)

Junior Mitglied
Benutzername: technic
Nummer des Beitrags: 6
Registriert: 08-2002
| | Veröffentlicht am Donnerstag, den 22. August, 2002 - 18:27: | 
|
Hallo Christian
Mein TI-89 gibt:
A=(2*cos(2x))/(4*x^2+1)
B=(1-2*cos(2x))*cos(e^(3*x-3*sin(2x)))
aber warum?! Und mit Maple gabs einen solchen Ausdruck!
Was machen wir da?
gruss Tec
|
    
Christian Schmidt (christian_s)

Erfahrenes Mitglied
Benutzername: christian_s
Nummer des Beitrags: 370
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 22. August, 2002 - 22:19: | 
|
Hmmm, aber meine Eingabe war doch korrekt oder?
diff(int(cos(t)/(1+t^2),t=17..2*x),x));
(Zu A)
MfG
C. Schmidt |
    
Tec (technic)

Junior Mitglied
Benutzername: technic
Nummer des Beitrags: 7
Registriert: 08-2002
| | Veröffentlicht am Freitag, den 23. August, 2002 - 07:55: | 
|
Wenn du fürs Integral dt nimmst stimmt das.
Ich habe jetzt (ev.) eine Lösung:
Für A:
Wenn ich zuerst die obere Grenze des Integrals ableite: diff(2x,x)=2 und dann dieses Resultat nur mit dem Ausdruck im Integral (t ersetzt durch die obere Grenze, also cos(2x)/(1+(2x)^2) multipliziere, erhalte ich genau das Resultat des TI. Das gleiche geht auch mit dem B. Warum ist mir aber nicht klar!
gruss Tec
|
    
clara

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 23. August, 2002 - 08:16: | 
|
Hi Tec,
habe mir was überlegt und zwar folgendes:
A: Bezeichne f(x) die Funktion im Integral und bezeichne F(x) eine Stammfunktion von f. Zu berechnen:
d/dx int(f(t),t,17,2x)
= d/dx (F(2x)-F(17)) = d/dx F(2x) - d/dx F(17).
Da F(17) eine Zahl ist, bleibt nach dem differenzieren hier eine 0.
Bleibt zu berechnen:
d/dx F(2x) = f(2x)*2 (Kettenregel)
= (2cos(2x))/(4x^2+1).
B ist zwar etwas kkomplizierter, aber müsste mit dem selben Prinzip gehen.
gruß clara |
    
Tec (technic)

Junior Mitglied
Benutzername: technic
Nummer des Beitrags: 8
Registriert: 08-2002
| | Veröffentlicht am Freitag, den 23. August, 2002 - 10:47: | 
|
Hi clara
Deine Begründung finde ich logisch, da
F(x) abgeleitet ja gerade wieder f(x) ergibt. Ich
habe B auch so gelöst, das funktioniert einwandfrei!
Besten Dank,
gruss Tec |