| Autor |
Beitrag |
    
Julia

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 30. Mai, 2002 - 15:48: | 
|
Hi!Wir behandeln gerade die Strahlensätze.
Hausaufgabe:Wir sollen beweisen,warum der 2. Strahlenstz nicht umkehrbar ist.
Es wäre nett,wenn du eine Begründung dazu schreiben würdest.
Danke |
    
...

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 06. Juni, 2002 - 14:32: | 
|
hm...also bei der antwort kann ich leider nich helfen, aber dafür bombadiere ich mit noch einer frage... was ist (bzw. wie lautet) der beweis für den 2. strahlensatz?? wie haben ihn nur für den 1. gemacht... |
    
Gast4

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 06. Juni, 2002 - 17:05: | 
|
Hallo Julia,
Der 2. Strahlensatz würde besagen:
(siehe Skizze)
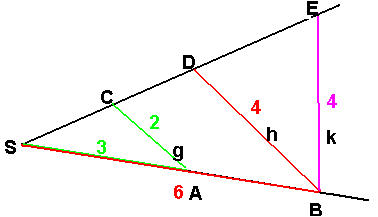
Wenn die Geraden g und h parallel sind, stehen die Strecken |SA| und |AC| im selben Verhältnis wie die Strecken |SB| und |BD|
(hier im Beispiel gilt also mit |SA|=3, |AC|=2, |SB|=6 und |BD|=4:
|SA|:|AC|=|SB|:|BD| )
Ich setze voraus, dass du den ersten Strahlensatz beherrschst:
Den ersten Strahlensatz kann man nun umkehren und
sagen:
"wenn die Verhältnisse der entsprechenden Strecken gleich groß sind, dann müssen die Geraden g und h parallel sein"
Díese Umkehrung würde auf den 2. Strahlensatz übertragen lauten:
"Wenn |SA|:|AC|=|SB|:|BD|, dann ist g||h."
Das gilt auch in dieser Skizze, aber es gilt auch noch:
|SA|:|AC|=|SB|:|BE|, wenn nun die Umkehrung des 2. Strahlensatzes gälte, könnte man sagen, dass g und k dann auch parallel sind.
Das sind sie aber offensichtlich nicht.
Also gilt die Umkehrung des 2.Strahlensatzes nicht.
|
    
...

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 06. Juni, 2002 - 18:32: | 
|
GIbt es denn keinen beweis ??? |
    
Ralf

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 06. Juni, 2002 - 19:16: | 
|
Dazu braucht man den 2. Strahlensatz nicht zu beweisen.
In dem Fall, dass gezeigt werden soll, dass etwas nicht gilt, reicht es aus, ein einziges Gegenbeispiel anzugeben.
Das wurde hier gemacht, und schon ist gezeigt, dass die Umkehrung des 2. Strahlensatzes nicht gilt.
Das war in diesem Fall der Beweis.
|
    
Gast2

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 07. Juni, 2002 - 00:43: | 
|
Hallo ...,
deine Frage bezog sich nur auf den 2en Strahlensatz, oder? Nicht darauf, dass die Umkehrung nicht gilt, denke ich mal...
Man kann den 2en Strahlensatz beweisen, in dem man mit ´in geeignetem Abstand´ (und genügend klein) gewählte parallele Geraden zu der obigen Gerade gegeben durch S,E wählt. Nun muß man wissen, dass parallele Geraden die immer denselben Abstand voneinander haben, nichtparallele Geraden im IR² immer in gleich große Stücke ´zerteilen´. Über die Anzahl der Stücke erhältst du dann den 2en Strahlensatz!
Z.B. würde die Strecke SB sich dann durch eine solche Unterteilung in m*x und SA in n*x (x= entsprechende Längeneinheit eines Stückes) aufteilen, während DB in m*x´ und CA in n*x´ aufgeteilt würden (x´ die andere entsprechende Längeneinheit eines Stückes).
Dann gilt:
SB/SA=m*x/(n*x)=m/n=m*x´/(n*x´)=DB/CA
Dies ist äquivalent zu
SA/CA=SB/DB
Tschau
Gast2 |
    
...

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 07. Juni, 2002 - 14:57: | 
|
HI Gast2 !!
Danke.. ja genau das meinte ich 
aber eine Frage hab ich noch..was istIR² ??und m ;n ??..danke im vorraus |
    
Gast2

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 07. Juni, 2002 - 19:12: | 
|
Hi ...,
m,n sind natürliche Zahlen. Das ist die Anzahl der einzelnen Längeneinheiten! Das meinte ich mit geeignetem Abstand. Der Abstand der Geraden muss so gewählt werden (zumindest für diesen Beweis), dass eine solche Aufteilung möglich ist. IR²? Sorry, in der 8-10 weiß man damit wahrscheinlich nix anzufangen. Im Prinzip meinte ich das 2 dimensionale Kartesische Koordinatensystem. Also x-Achse nach rechts, y-Achse senkrecht auf die x-Achse und beide mit der Längeneinheit 1cm.
Im 3-dimensionalen müssen sich 2 Geraden, die nicht parallel sind, nämlich nicht schneiden. So genannet windschiefe Geraden!
Damit du nochmal verstehst, wie du Vorgehen mußt:
Angenommen, SA wäre 1,8 cm und AB wäre 2,1cm. Wir suchen eine Längeneinheit x so, dass es m und n aus IN gibt, so dass n*x=1,8 und m*x=3,9 (da SA+AB=3,9). Mit x=0,3 haben wir eine solche Längeneinheit gefunden (PS: x muß nicht immer rational sein, habe ich hier extra so gewählt!). Nun ist also m=3,9/0,3=13. Also unterteilst du SB in m=13 Stücke der Längeneinheit x=0,3cm. Nun legst du durch alle diese Punkte jeweils zu SE parallele Geraden an. Dann wird auch die Strecke DB in m=13 gleichlange Stücke unterteilt (mit anderer Längeneinheit, nämlich x´). Ebenso haben wir ja SA in n=1,8/0,3=6 Stücke unterteilt mit der Längeneinheit x=0,3cm. Die Strecke CA wird durch die Parallelen auch in n=6 gleichlange Stücke unterteilt (mit der anderen Längeneinheit x´).
Tschau
Gast2 |
|