| Autor |
Beitrag |
    
franz

| | Veröffentlicht am Freitag, den 19. Mai, 2000 - 12:05: | 
|
Um freundliche Unterstützung in der Privatfrage, wie man das Kugelvolumen im R4, oder vielleicht auch höher, ermittelt, bittet F. |
    
Fern

| | Veröffentlicht am Freitag, den 19. Mai, 2000 - 17:43: | 
|
Hi franz,
Hier die Formel: (habe ich aus einem Mathe-Buch)
Volumen einer n-dimensionalen Hyperkugel:
pin/2
V = -------- * rn falls n gerade.
(n/2)!
2npi(n-1)/2 * [(n-1)/2]!
V = ------------------------- * rn
n!
falls n ungerade.
Für n = 4 ergibt dies: V = pi²r4/2
============
für n=3: V = (4/3)pi*r³
Frag mich aber nicht, wie man zu diesen Formeln kommt!
Gruß, Fern
|
    
reinhard (Gismo)

| | Veröffentlicht am Freitag, den 19. Mai, 2000 - 19:42: | 
|
Hallo Fern und Franz!
Man kommt zu dieser Formel über die Integration!
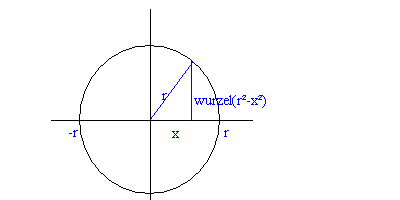
Zuerst überlegen wir uns, wie man zum Flächeninhalt im 2-Dimensionalen kommt:
Man integriert von -r nach r die senkrechten Linien, deren Länge abhängig von x ist, nämlich 2*Ö(r²-x²)
Die Kreisfläche ist also
V2 = ò-r r2Ö(r²-x²)dx = 2ò-r rÖ(r²-x²)dx = wie in jeder guten Formelsammlung zu finden ist 2(x/2Ö(r²-x²)+r²/2*arcsin(x/r))|-rr = 2(0+r²/2*p/2-0+r²/2*p/2)=r²p
Wenn man nun eine Kugel berechen will, kann man wieder dieselbe Skizze nehmen, nur handelt es sich dann nicht um Striche, die aufintegriert werden, sondern um Kreisscheiben, deren Radius jeweils Ö(r²-x²) beträgt.
Also
V3 = ò-r r(Ö(r²-x²))²pdx = ò-r r(r²-x²)pdx=p(r²x-x³/3)|-rr=p(r³-r³/3+r²-r³/3)=4r³p/3
Um dann das Volumen einer 4-Dimensionalen Kugel zu berechnen, darf man sich nicht allzuviel vorstellen, sondern muß einfach ganz strickt in dieser Art und weise weiterrechnen: man integriert von -r nach r die Volumina von Kugeln, deren Radius Ö(r²-x²) beträgt:
V4 = ò-r r4p/3*Ö(r²-x²)3dx = 4p/3*ò-r rÖ(r²-x²)3 =
Entweder man findets in einer Formelsammlung oder man teilt das in (r²-x²)*Ö(r²-x²) und nimmt die Produktformel für die Integration
=4p/3(x/4*Ö(r²-x²)3+3r²x/8*Ö(r²-x²)+3r4/8*arcsin(x/r))|-rr = 4p/3(0+0+3r4p/16-0-0+3r4p/16) = r4p2/2
usw........
bei geraden n ist die Integration einfacher (weil dann die Wurzel bei Ö(r²-x²) wegfällt) - man merkt es in der von Fern angegebenen Formel -, aber bei ungeraden n ist es auch nicht weiter schwer (einfach in ein Produkt zerlegen und dann mit der Produktregel). Es wird nur dementsprechend umständlicher und länger, je größer das n wird.
Wenn man das ganze dahinintegriert fällt bald die Gesetzmäßigkeit auf, ich kann also bis zu V10 diese Formel nur bestätigen, aber einen Beweiß, daß sie für alle n gelten, habe ich leider auch nicht.
Reinhard |
    
H.R.Moser,megamath.

| | Veröffentlicht am Samstag, den 20. Mai, 2000 - 20:48: | 
|
Hall0 Franz,
Sehr viel Prominenz hat sich bereits Deiner Frage nach dem
Volumen der Hyperkugel gewidmet und diese prinzipiell beantwortet.
Gleichwohl möchte ich auch zu diesem illustren Kreis stossen, um eine
Bemerkung zum Beweis der allgemeinen Formel für das Volumen
V(n) einer Kugel des Rn anzubringen
Diese Formeln können (gegenüber den Formeln von Fern leicht modifiziert)
für R als Kugelradius so geschrieben werden :
(I) gerade n ; n = 2*m
V(2m) = 1 / m! * Pi ^ m * R ^ ( 2 m)
(II) für ungerade n ; n = 2m + 1
V(2m+1) = 2^( m + 1) / [3 * 5 * 7 .. * (2m+1)] * (Pi)^m * R^(2m+1)
Gültig für alle natürlichen Zahlen m = 1, 2, 3 ...
Der Beweis gelingt durch vollständige Induktion nach m
Es ist nutzbringend , wenn man dabei von den folgenden
Rekursionsformeln Gebrauch macht:
V(2m) = 2 * R * V(2m-1) * ( int( cos ^ ( 2m) (t) dt) ), Grenzen 0 bis Pi/2
Also
V(2m) = 2 * R * V(2m-1) * [(2m-1)*/2m-3) .. 1 ] / [2m(2m-2) ..*2] * Pi /2
Verankerung: V(1) = 2* Pi * R
(Formel R1)
V(2m+1) = 2 * R * V(2m)* (int ( cos^(2m+1) (t) dt )), dieselben Grenzen
Also:
V(2m+1) = 2 * R * V(2m) [2m(2m-2)3.. *2] / [(2m+1)*(2m-1).. *1]
Verankerung : V(2) = Pi * R ^ 2
(Formel R2)
Anmerkung
Zu den Integralen der Kosinuspotenzen gelangen wir ,
indem wir in den Integralen ,die Reinhard angeschrieben hat, die folgende Substitution ausführen:
r = R* cos t , z = R* sin t , dz = R cos t dt
für z = 0 gilt t = 0 , für z = R gilt t = Pi / 2
So erhalten wir z.B.:
V(4) = 2 * (int ( 4*Pi * r^3 / 3 * dz) ,Grenzen 0 bis R
= 8* Pi / 3 * (int (R^2 - z^2) ^(3/2) *dz) ,dieselben Grenzen
= 8 * Pi * R ^ 4 / 3 * (int cos^4 (t) * dt),Grenzen 0 bis Pi/2
Zum Schluss folgen die ersten paar V-Werte für ungerade Dimensionszahlen:
V(5) = 8 / 15 * Pi ^ 2 * R^5
V(7) = 16 / 105 * Pi ^ 3 * R^7
V(9) = 32 / 945 * Pi ^ 4 * R ^9
Ich glaube , diese Mitteilungen sollten genügen
Zu weiteren Taten bin ich aber gerne bereit
Bis dann: freundliche Grüsse an alle
H.R. |
    
franz

| | Veröffentlicht am Montag, den 22. Mai, 2000 - 10:36: | 
|
Hallo Fern, Reinhard und megamath, für die massiven n-dimensionalen Information bedanke ich mich herzlich!
Mein Verständnis-Problem ist leider elementarer, vielleicht durch zuviele Gespenstergeschichten induziert: Der Übergang zum Vierdimensionalen. Die Kreis- und Kugelberechnungen sind natürlich in sich vollkommen schlüssig; aber irgendwie "zu" anschaulich.
Wie begründet man, daß jetzt über bestimmte Kugeln zu integrieren sei? Was haben die mit der R4-Kugel zu tun, geometrisch oder analytisch? (Habe selber diese Linie verfolgt, mittels Polar- beziehungsweise spärischen Koordinaten jeweils Umfang/Oberfläche der Figuren zu bestimmen und von daher Fläche/Volumen. Schön und gut, aber: wie weiter? Die R4-Oberfläche müßte doch ein R3-Volumen sein??).
Freundliche Grüße & um Verständnis bittend, Franz. |
|