| Autor |
Beitrag |
    
KML
Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 10:18: | 
|
Hi, ich muss bei folgender Aufgabe das Integral auf ein Grundintegral zurückführen und dann integrieren. Als Ansatz wird als Substitution t = tan x/2 genannt, aber irgendwie komme ich damit nicht weiter... Ergebnis ist 7,7
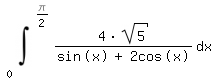
Danke für jede Antwort! |
Orion (Orion)
Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 1025
Registriert: 11-2001
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 13:17: |
|
KML,
sin(x)+2 cos(x) =
sqrt(5)*[(1/sqrt(5) sin(x) + (2/sqrt(5))cos(x)]=
sqrt(5)*sin(x+ j) , j=tan(2)
Das gesuchte Integral ist also
4*ò0 greek{p/2} dx/sin(x+p)=
4*òj p/2+j du/sin(u)
mfG Orion
|
Orion (Orion)
Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 1026
Registriert: 11-2001
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 13:20: |
|
KML,
sin(x)+2 cos(x) =
sqrt(5)*[(1/sqrt(5) sin(x) + (2/sqrt(5))cos(x)]=
sqrt(5)*sin(x+ j) , j=tan(2)
Das gesuchte Integral ist also
4*ò0 p/2 dx/sin(x+p)=
4*òj p/2+j du/sin(u)
Es ist aber
ò du/sin(u) = ln | tan(u/2)| + C
mfG Orion
|
KML
Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 14:23: |
|
Erstmal vielen Dank für Deine Antwort, aber wie kommst Du darauf, das der Ausdruck 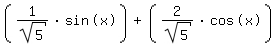 =  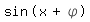ist? Und warum ist phi = tan(2). Und hat es eine Bedeutung das du unten statt phi pi nimmst?
Danke nochmal. Wäre super wenn Du für die Gleichungen folgende Seite benutzen könntest: http://fed.optimath.com/freehtml.php |
Megamath (Megamath)
Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 5130
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 14:40: |
|
Hi KML
Wenn Du Interesse am formalen Ergebnis J Deiner Aufgabe
hast,gebe ich dieses gerne bekannt.
Das Resultat in der konzentriertesten Form lautet:
J = 16 ln (tau) mit tau = (sqrt(5)+1)/2
tau: : cf. goldener Schnitt!
Gruss H.R.Moser,megamath |
KML
Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 15:12: |
|
sorry, aber das sagt mir leider grad garnichts |
Orion (Orion)
Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 1027
Registriert: 11-2001
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 16:18: |
|
KML,
Wenn man einen Term der Form
f(x) = a sin(x) + b cos(x)
hat, so kann man ihn in der Form
f(x) = A sin(x+j)
schreiben. Nach dem Additionstheorem lautet
nämlich die rechte Seite
f(x) = A cos(j)sin(x) + A sin(j)cos(x)
Es muss alo gelten
A cos(j) = a , A sin(j) = b
=> A2 = a2+b2 , tan(j) = b/a
In unserem Fall ist a=1, b=2 => A=sqrt(5),
tan(j) = 2.
Variante : Substituiere
x = 2 arctan(t) => sin(x) = 2t/(1+t2),
cos(x) = (1-t2)/(1+t2), dx = 2t/(1+t2)*dt
Der Integrand ist dann bis auf einen Zahlfaktor von der Form
1/(t2-t-1)
und man kann Partialbruchzerlegung anwenden.
mfG Orion
|
Megamath (Megamath)
Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 5131
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 16:39: |
|
Hi
Ich meinte das Folgende:
Mir sagt die Angabe Deines Resultats(7,7), eine grobe Naeherung,auch gar nichts.
Meine Angabe beschreibt das Ziel, das Du erreichen solltest.
Da Orion Dir zur Genuege geholfen hat, solltest Du dieses Ziel
erreichen, ohne weitere Hilfe.
Des Weiteren ist es in diesem Forum ueblich, sich nicht nur
an die Fragesteller zu wenden, sondern an alle,
die Interesse an der Materie haben.
Eine weitere Forumsregel: man sagt Danke!
Gruss
H.R. |
KML
Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 19:35: |
|
Diese Forenregel ist mir durchaus bekannt und ich habe mich bei Orion bedankt, wenn Du Dir meinen Post nochmal ansehen würdest.
Nur da ich zwischen Deinem Post und meiner weitergehenden Frage nicht den geringsten Zusammenhang erkennen konnte, war ich etwas verwirrt.
Trotzdem danke nochmal, besonders an Orion (auch wenn ich immer noch nicht ganz dahinter gekommen bin) |
Megamath (Megamath)
Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 5132
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 19:56: |
|
Hi KML
Berechne die beiden Nullstellen im Nenner des Bruches 1 /(t^2-t-1),
den Orion angegebne hat.
Du benötigst diese Zahlen bei der Partialbruchzerlegung.
Eine dieser Nullstellen ist die von mir im Endresultat angegebene Zahl
tau aus dem goldenen Schnitt, die andere hängt eng damit zusammen.
Das ist der Zusammenhang mit meiner Bemerkung,
die offenbar nach und nach klar wird, jedoch zu früh im Forum erschien.
Sie könnte noch zu einem AHA-Erlebnis führen!
Gruss
HRM |
Orion (Orion)
Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 1028
Registriert: 11-2001
| | Veröffentlicht am Mittwoch, den 18. Mai, 2005 - 21:59: |
|
Noch ein Tipp : Rechne nach, dass
1-t-t2 = (5/4){1 - [(2t+1)/sqrt(5)]2}
und substituiere daraufhin
(2t+1)/sqrt(5) =: u.
Dann stösst Du auf das "Grundintegral"
ò du/(1-u2) = artctanh(u) =
(1/2)ln[(1+u)/(1-u)]
PM:
arctanh(u) ist die Umkehrfunktion des hyperbolischen
Tangens :
tanh(u) := sinh(u)/cosh(u)
= (eu-e-u)/(eu+e-u)
(Beitrag nachträglich am 18., Mai. 2005 von orion editiert)
mfG Orion
|
Megamath (Megamath)
Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 5133
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 19. Mai, 2005 - 21:17: |
|
Hi allerseits
Aufmerksame Teilnehmer am Forum haben mich gebeten,
die von mir beiläufig erwähnte Lösung zu dem von KML
vorgelegten bestimmten Integral rechnerisch im Détail
herzuleiten.
Das will ich gerne tun.
Vorgängig zeige ich ein paar Grundrechnungen, die mit den
beiden in Theorie und Praxis des goldenen Schnitts
auftretenden Termen r und s von Nutzen sind.
Es sei r = [sqrt(5) - 1] / 2 ; s = [sqrt(5) + 1] / 2.
Dann gilt das Folgende:
s = r + 1 ; r * s = 1 ; r + s = sqrt (5) usw.
Wir betrachten den durch die Substitution t = tan (x/2)
für die Integration nach t vorbereiteten Integranden g(t) :
g(t) = 4 * sqrt(5) * h(t)
mit
h(t) = - 1 / [t^2 – t -1]
Die Nullstellen des Nenners sind t1 = s , t2 = - r.
Wir setzen die Partialbruchzerlegung von h(t) so an:
h(t) = A / (t – s) + B / (t+r) und finden durch
Koeffizientenvergleich:
A = - 1 / sqrt(5), B = 1/sqrt(5)
Der Integrand g(t) wird dadurch zu
g(t) = 4 * [ - 1 / (t – s) + 1 / (t + r) ]
Das gibt beim Integrieren wohlvertraute Logarithmen,
wobei wir daran denken, die Absolutbeträge unter dem
Log-Symbol zu nehmen.
Wenn wir ein bestimmtes Integral berechnen wollen,
ist eine Rücktransformation nicht notwendig:
der unteren Grenze x = 0 entspricht die untere Grenze t = 0
zu der oberen Grenze Pi/2 in x gehört die obere
Grenze 1 bezüglich t
Einsetzen der Grenzen liefert das gesuchte Integral J:
J = 4* [ln ((s/r) – ln (r/s)] =
4* ln [ (s/r)^2 ] = 8 * ln [ s/r ] = 8* ln ( s^2 )
= 16 * ln (s); voilà!
Gruss
HRM |
