| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3104
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 26. November, 2003 - 17:34: | 
|
Hi allerseits

Die Aufgabe LF 119 steht zum Ausgleich der
früheren Aufgabe 117, die etwas zu leicht war;
sie lautet:
Die n Zahlen a1, a2,….,ak,……,an sind positiv und
alle voneinander verschieden, ihre Summe sei S.
R sei die Summe aller Reziprokwerte der aj ; T die
Summe der bk = ( n - 1 ) / ( S – ak ) mit
k = 1 bis n.
Man beweise die Ungleichung
R > T
mit Hilfe der Ungleichung vom arithmetischen
Mittel A und harmonischen Mittel H.
Mit freundlichen Grüßen
H.R.Moser, megamath
|
    
Martin243 (Martin243)

Senior Mitglied
Benutzername: Martin243
Nummer des Beitrags: 909
Registriert: 02-2001
| | Veröffentlicht am Donnerstag, den 27. November, 2003 - 00:08: | 
|
Hi!
Ja, die war schon schwerer. Schon erstaunlich, wie lange man dafür braucht in Anbetracht der Lösung (die hoffentlich keine Fehler enthält...):
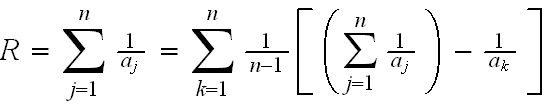
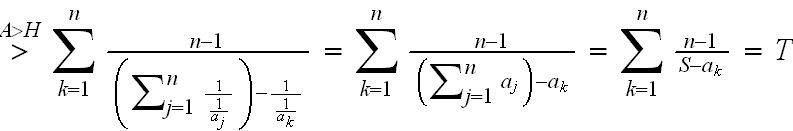
Jetzt kann ich endlich ins Bett gehen, muss morgen eine Mathe-Klausur schreiben, äääh, heute...
MfG
Martin
________
Die Natur spricht die Sprache der Mathematik:
Die Buchstaben dieser Sprache sind Dreiecke, Kreise und andere mathematische Figuren.
Galileo Galilei
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3105
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 27. November, 2003 - 08:01: | 
|
Hi Martin.
Deine Lösung ist korrekt.
Zum Vergleich zeige ich Dir meine etwas ausgefallene Lösung,
die i.a. nicht schlecht ankommt.
Weitere Aufgaben zum Thema werden folgen.
In welchem Institut musst Du denn Klausuren schreiben?
Ich nehme an, dass Du auch dort Erfolg hast!
Zur Lösung der Aufgabe LF 119 benützen wir,
wie gewünscht, den Satz vom harmonischen Mittel H
und arithmetischen Mittel A, der bekanntlich die Ungleichung
1/H < A beinhaltet.
Bei der Anwendung dieses Satzes lassen wir ak weg, so dass die
Formel auf die übrigen n-1 Elemente angewendet wird, ein
nützlicher Trick, wie sich zeigen wird.
Es entsteht mit H > 1/A die Ungleichung
1/(n - 1) { [1/a1+1/a2+……+1/an] - 1/ak} > ( n - 1) / (S – ak)
Jetzt schreiben wir für alle k = 1 ..n diese Zeilen schön
untereinander und addieren.
Die Summe über die eckige Klammer ist n*R, diejenige
der Einsiedlerkrebse 1/k hinter dem Minuszeichen ist R .
Damit ergibt sich:
1 / (n-1) { n * R – R} = sum[( n – 1 ) / (s – ak)], k=1..n.
Die geschweifte Klammer ist (n-1)*R, so dass links nur
R übrig bleibt.
Damit ist die Behauptung bewiesen!
MfG
H.R.Moser,megamath |
|