| Autor |
Beitrag |
    
Elsa13 (Elsa13)

Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 30
Registriert: 12-2002
| | Veröffentlicht am Dienstag, den 21. Oktober, 2003 - 20:12: | 
|
Hallo!
Ich komme nicht weiter beim Abschätzen...
Gegeben ist die Folge:
(xn) = (1 + 1/ n ^ 2) ^ n
Man untersuche das Konvergenzverhalten und bestimme gegebenenfalls den Grenzwert.
Hinweis: Bernoulli’sche Ungleichung
Kann mir bitte jemand weiterhelfen?
elsa
|
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 1585
Registriert: 02-2002
| | Veröffentlicht am Dienstag, den 21. Oktober, 2003 - 21:23: | 
|
KENN GRENZWERT NICHT
aber konvergent ist xn sicher, da ja (1 + 1/n)^n -> e
gilt
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Elsa13 (Elsa13)

Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 31
Registriert: 12-2002
| | Veröffentlicht am Dienstag, den 21. Oktober, 2003 - 21:36: | 
|
hallo Fritz!
Ich weiß, daß der limes = 1 ist!
Der Beweis geht mit Bernoulli und dem Reziprokwert.
Aber wie gesagt, ich stehe an!
Liebe Grüße
elsa |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2845
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 21. Oktober, 2003 - 22:04: | 
|
Hi elsa,

Damit Du ruhiger schlafen kannst:
Nimm Deine n-te Potenz in den Sandwich
und schreibe die Ungleichung:
1+1/n < (1+1/n^2) ^ n < 1/ (1 – 1/n), n = 2 ,3 ,4….
Ganz links und ganz rechts geht’s gegen 1,
und ich gehe zu Bett, sk.
Fortsetzung morgen!
Mit herzlichen Grüßen
|
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 1586
Registriert: 02-2002
| | Veröffentlicht am Dienstag, den 21. Oktober, 2003 - 22:18: | 
|
Bernulli sagt mir nichts,
aber
wie wärs, den ln des Limes zu berechnen
n*ln(1 + 1/n²), form "Unendlich*0"
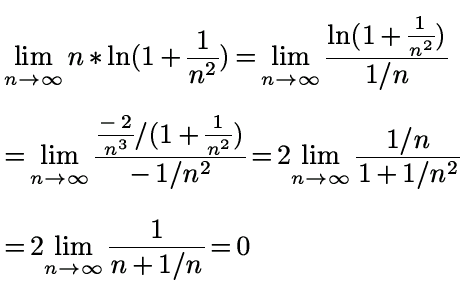
also
ln( Grenzwert ) = 0
Grenzwert = 1
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Elsa13 (Elsa13)

Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 32
Registriert: 12-2002
| | Veröffentlicht am Mittwoch, den 22. Oktober, 2003 - 04:00: | 
|
Ich danke Euch herzlich für die nächtlichen Ideen, ich werde sie studieren!
Guten Morgen!
elsa |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2846
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 22. Oktober, 2003 - 08:59: | 
|
Hi elsa

In einem ersten Abschnitt zur Lösung Deiner
Aufgabe beweisen wir einen Hilfssatz, bei welchem
eine zur Bernoullischen Ungleichung analoge
Ungleichung erscheint.
Diese Ungleichung (M) für natürliche Zahlen
n = 1,2 ,3…und für 0 < a < 1/n lautet:
(1 + a) ^ n < 1 / (1 – n a)………………………………(M)
°°°°°°°°°°°°°°°°°°°°°°°°°
Zum Beweis verwenden wir die Identität
( u ^ n – v ^ n ) / ( u – v ) = u^(n-1) +u^(n-2)*v +…+v^(n-1)
u – v ungleich null; Nachweis: geometrische Reihe.
Setze nun u = 1 + a, v = 1; es kommt
[(1 + a) ^ n – 1] / a < n (1+a) ^ (n-1) < n (1+a) ^ n
Wir lösen nach (1+a) ^ n auf; es entsteht die Ungleichung (M).
Fortsetzung folgt
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2847
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 22. Oktober, 2003 - 09:27: | 
|
Hi elsa

In diesem letzten Abschnitt beweisen wir die
wesentliche Ungleichungskette zur Lösung
Deiner Aufgabe; sie lautet
1+1/n < (1+1/n^2) ^ n < 1/ (1 – 1/n), n = 2 ,3 ,4
Wir benötigen dazu die Bernoullische Ungleichung
(1 +a)^n > 1 + na , für n = 2, 3 ,4 und a > 0.
Wir setzen darin a = 1/ n^2 und erhalten
(1+1/n^2) ^ n > 1 + 1/n…………………………….(B)
Weiter benötigen wir die im ersten Abschnitt
hergeleitete Ungleichung (M):
(1 + a) ^ n < 1 / (1 – n a)……………………………(M)
Wir setzen wiederum a =1 /n^2; es entsteht:
(1+1/n^2) ^ n < 1 / (1 – 1/n) = n / ( n - 1 )
Damit ist alles nachgewiesen.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2849
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 22. Oktober, 2003 - 10:41: | 
|
Hi elsa

Zu Vergleichszwecken wollen wir noch die Aufgabe lösen,
für die Folge der xn mit
xn = (1 - 1/n^2) ^ n
das Konvergenzverhalten zu untersuchen und einen
allfälligen Grenzwert zu bestimmen.
Von der Eulerschen Zahl e darf kein Gebrauch
gemacht werden.
Die Hauptaufgabe besteht darin, xn nach
unten abzuschätzen
Das Ergebnis wird sein:
1 – 1 / n < xn………………………………………(Y)
Nach oben : trivialerweise gilt xn < 1
xn ist wiederum im Sandwich, der Grenzwert ist 1.
Eine Herleitung der Ungleichung Y folgt !*
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 2850
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 22. Oktober, 2003 - 14:01: | 
|
Hi elsa

Um die Ungleichung (Y) zu beweisen, verwenden wir
die Ungleichung (B) von Bernoulli.
Wir schauen genau hin auf die folgende Zeile:
(1 + a) ^ n > 1 + a * n………………………………………(B)
gültig für alle a € R mit a > - 1
und alle natürlichen Zahlen > 1
a = - 1 / n^2 erfüllt die Bedingung und mit (Y) entsteht
die gewünschte Ungleichung:
1 – 1/ n < (1 – 1 / n^2 ) ^ n………………………………...(YM)
Wir sind am Ziel
Mit freundlichen Grüßen
|
    
Elsa13 (Elsa13)

Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 33
Registriert: 12-2002
| | Veröffentlicht am Donnerstag, den 23. Oktober, 2003 - 04:00: | 
|
ja - danke, ich noch nicht ganz,
ich werde es noch einmal durchdenken!
liebe Grüße
elsa |