ZahlReich - Mathematik Hausaufgabenhilfe: Grenzverhalten

Grenzverhalten

ZahlReich - Mathematik Hausaufgabenhilfe » Klassen 12/13 » Funktionen » Grenzwerte » Grenzverhalten « Zurück Vor »

Das Archiv für dieses Kapitel findest Du hier.

Autor

Beitrag

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 86
Registriert: 03-2001

Veröffentlicht am Samstag, den 30. August, 2003 - 16:27:

hi! geht um folgende aufgabe: lim x->7 (2 - ‹(x - 3))/(x^2 - 49) Hinweis: erweitern sie...
grüße
BoM

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1333
Registriert: 02-2002

Veröffentlicht am Samstag, den 30. August, 2003 - 16:37:

Wie lautet der Zähler Wirklich?

Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 87
Registriert: 03-2001

Veröffentlicht am Samstag, den 30. August, 2003 - 16:57:

ups sorry

lim x->7 (2 - sqrt(x - 3))/(x^2 - 49)

ist richtig

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1334
Registriert: 02-2002

Veröffentlicht am Samstag, den 30. August, 2003 - 17:51:

also ich würde x = 7+d substituieren ( das entspricht bloß einer "Verschiebung entlang der x-Achse"
dann ist es
lim_d->0(2-sqrt(4+d))/(d²+14d)
und
nur L'Hospital anwendenen
also
lim_d->0(-1/[2*sqrt()])/(2d+14) = -1/(2*2*14)

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 88
Registriert: 03-2001

Veröffentlicht am Samstag, den 30. August, 2003 - 18:14:

L'Hospital hatten wir aber noch net :-(

der lässt sich sicher auch net in 2-3 sätzen erklären oder?

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1335
Registriert: 02-2002

Veröffentlicht am Samstag, den 30. August, 2003 - 18:15:

der Tip
mit der Erweiterung meint wohl mit 2+sqrt()
zu erweitern
also
lim_x->7(7-x)/[(x²-7²)(2+sqrt())]
= -lim_x->7(7-x)/[(x+7)(x-7)(2+sqrt())]
=-lim_x->7(1/[(x+7)(2+sqrt())]
was
zum gleichen Ergebenis führt.

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 89
Registriert: 03-2001

Veröffentlicht am Sonntag, den 31. August, 2003 - 09:41:

ah mist warn vorzeichenfehler... danke :-)

hab aber nun nen neues problem:
lim x->0 (1-cos x)/(x*((sqrt(1+x))-1))

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1338
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 10:21:

Das kannst Du nun aber wirklich selbst.
Mach den Nenner rational, erweitere als mit
x*sqrt()+1
--------------------------
im
Übrigem rate ich Dir,
dich bei
http://mathdraw.hawhaw.net
umzusehen:
Schöne darstellung von Formel,
schrittweise Erklärung beim Differenzieren
und Integrieren
Berechnung von Grenzwerten
Kurvendiskussion!!

(Beitrag nachträglich am 31., August. 2003 von friedrichlaher editiert)

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 90
Registriert: 03-2001

Veröffentlicht am Sonntag, den 31. August, 2003 - 11:01:

wenn ich mit dem term erweiter hab ich ja
(x*sqrt(1+x)-cosx*x*sqrt(1+x)+1-cosx)/(x^3) da aber x gegen 0 läuft hab ich ja 1/0 was ja nu nicht geht :-(

wie krieg ich das x^3 weg?

dein link hat mir den grenzwert 1 vorrausgesagt, nur leider hat er mir nicht verraten wie er dazu kommt ;)

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1340
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 11:42:

Du brauchst im Zähler nicht "auszumultiplizieren",
und er wird nach wie vor 0;
und
im Nenner erhälts Du
x²(1+x)-1 also = -1 für x -> 0

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 91
Registriert: 03-2001

Veröffentlicht am Sonntag, den 31. August, 2003 - 11:50:

hm dann wäre der grenzwert aber 0/-1 also 0 und laut derive müsste da 1 als grenzwert sein... ist der nenner nicht x^2*((1+x)-1) also somit auch gleich 0?

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1343
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 12:29:

also, mathematica sagt 0
umd mathdraw auch

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1344
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 12:31:

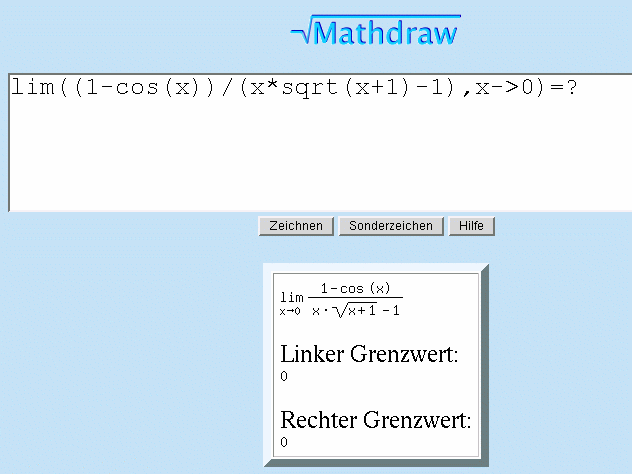
oder mißverstehen wir uns bezüglich der Aufgabe?
grw

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 92
Registriert: 03-2001

Veröffentlicht am Sonntag, den 31. August, 2003 - 12:57:

im Nenner ist noch ne klammer,dann sieht das so aus:
anlage1

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1345
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 13:30:

erweiter dann also nicht nur mit
sqrt(x+1)-1 sondern auch mit
(1+cos(x))
Darf der Grenzwert
lim_x->0(sinx / x) = 1
schon vorausgesetz werden?

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 93
Registriert: 03-2001

Veröffentlicht am Sonntag, den 31. August, 2003 - 13:36:

ja das hatten wir schon "bewiesen", nur wie kriegt man den sinus da rein? wenn ich mit sqrt(x+1)+1 erweiter hab ich ja: ((1-cos(x))(sqrt(x+1)+1))/(x^2)

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1346
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 13:42:

(1-cosx)(1+cosx)= 1-cos²x = sin²x,
und
im Nenner steht x², also (sinx/x)²*(...)

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 94
Registriert: 03-2001

Veröffentlicht am Sonntag, den 31. August, 2003 - 13:44:

ah da war schon jemand schneller ;) besten dank, jetzt hab ichs :-)

(Beitrag nachträglich am 31., August. 2003 von BoM editiert)

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1347
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 13:59:

ich hoffe, das

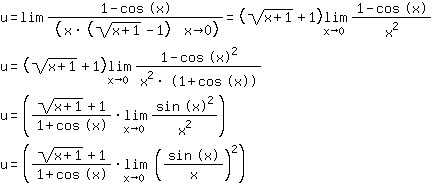
ist nun klar

Bom (bom)

Fortgeschrittenes Mitglied
Benutzername: bom

Nummer des Beitrags: 95
Registriert: 03-2001

Veröffentlicht am Sonntag, den 31. August, 2003 - 14:42:

vielen dank für deine mühe :-)

sag mal, gibts eigentlich ein programm was diese einzelnen rechenschritte so ausgibt?
grüße
BoM

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1348
Registriert: 02-2002

Veröffentlicht am Sonntag, den 31. August, 2003 - 15:39:

ist mir leider nicht bekannt.
Hab aber beim Author von mathdraw schon mal
angefragt.

Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher

Nummer des Beitrags: 1351
Registriert: 02-2002

Veröffentlicht am Montag, den 01. September, 2003 - 08:25:

Bom hatte mich, per ICQ, dann auch noch um Hilfe
bei
lim_x->pi/4( sqrt(2) - 2cosx ) / (sqrt(2) - 2sinx)

gebeten.( OHNE L'Hospital )
Da es auch mir zunächst schwer fiel, sei es hier
dargestellt
Ich kürze ab:
w = Quadratwurzel aus 2
s = sin(x)
c = cos(x)
damit wird der Ausdruck, für den der Grenzwert
gesucht ist zu


(w - 2c)/(w - 2s)	=	1 +	2(s - c)/(w - 2s)
(s - c)/(w - 2s)	=	(s - c)	(w + 2s)/[(w + 2s)(w - 2s)]
	=	(s - c)	(w + 2s)/(2 - 4s²)
	=	(s - c)	(w + 2s)/[2(1-2s²)]
2(s -c)/(w - 2s)	=	(s - c)	(w + 2s)/[(1-s²)-s²]
	=	(s - c)	(w + 2s)/(c² - s²)
	=	(s - c)	(w + 2s)/[(c+s)(c-s)]
	=	-	(w + 2s)/(c + s)
(w - 2c)/(w - 2s)	=	1 -	(w + 2s)/(c + s)

Setzt man nun für
w = Quadratwurzel(2),

s = c = sin(pi/4) = w/2 ein
ergibt sich

lim_x->pi/4( sqrt(2) - 2cosx ) / (sqrt(2) - 2sinx) = -1

Administration Abmelden Previous Page Next Page