| Autor |
Beitrag |
    
Rene

| | Veröffentlicht am Samstag, den 06. Oktober, 2001 - 11:06: | 
|
Der auf der positiven 1. achse liegende scheitel der hyperbel hyo: x²-y²=1 ist Mittelpunkt eines Kreises mit dem Radius r=2. Die Hyperbel und der Kreis rotieren um die 1 achse wobei ein rotationshyperboloid und eine kugel entstehen. wieviel prozent vom volumen der kugel sind die volumina der teile, in die die kugel durch das hyperboloid zerlegt wird? |
    
Araiguma (Uwe)

| | Veröffentlicht am Samstag, den 06. Oktober, 2001 - 11:57: | 
|
Willst du alles vorgerechnet haben oder kannst du deine Frage etwas spezifizieren?
Rotationskörper: pi integral f2dx |
    
Rene

| | Veröffentlicht am Sonntag, den 07. Oktober, 2001 - 09:20: | 
|
Ich weiss nicht wie ichs rechnen soll....sorry |
    
Araiguma (Uwe)

| | Veröffentlicht am Sonntag, den 07. Oktober, 2001 - 13:48: | 
|
Hallo Rene,
die Hyperbel und der Kreis haben nach y umgestellt die Funktionen (w=Wurzel, r=2):
y = f(x) = w(x2 - 1)
y = g(x) = w(r2 - x2)
Die Kugel und das Rotationshyperbolid ergeben sich dann mit:
pi int(f(x)2 dx, a, b) und
pi int(g(x)2 dx, a, b)
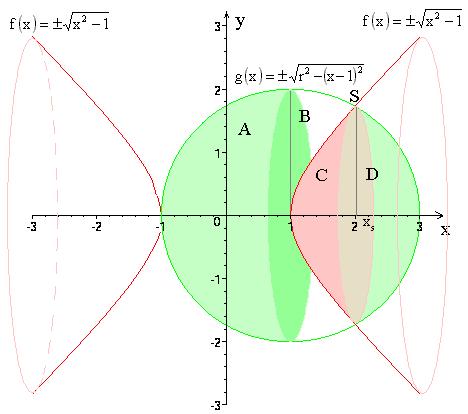
a und b sind dabei die Grenzen, die man bei der Kugel normalerweise auf a=-r und b=+r setzt. Hier muss die Kugel aber in verschiedene Segmente unterteilt werden. Ich habe dies in untenstehender Zeichnung verdeutlicht. Volumen A, B sind außerhalb und C, D sind Volumen innerhalb des Hyperboloiden.
Das Quadrieren hebt glücklicherweise gerade die Wurzeln in den Funktionen auf, so daß die Integration nicht so schwer ist.
Kugel:
pi int(r2 - x2 dx, a, b)
= pi [r2x - x3/3, a, b]
Hyperboloid:
pi int(x2 - 1, a, b)
=pi [x3/3 - x, a, b]
Für die Volumen C und D müssen wir dann xs des Schnittpunktes S ermitteln:
w(4 - (x-1)2) = w(x2 - 1)
4 - (x-1)2 = x2 - 1
4 - x2 + 2x - 1 = x2 - 1
0 = 2x2 - 2x - 4
0 = x2 - x - 2
0 = (x - 1/2)2 - 9/4
9/4 = (x - 1/2)2
+- 3/2 = x - 1/2
x1,2 = 1/2 +- 3/2
x1 = 2
x2 = -1
Jetzt kannst sicherlich die Volumen berechnen:
A = pi [r2x - x3/3, -1, 1] eine Halbkugel
C = pi [x3/3 - x, 1, 2]
B = pi [r2x - x3/3, 1, 2] - C
D = pi [r2x - x3/3, 2, 3]
Dann musst du noch das gesamte Kugelvolumen K mit den Teilen ins Verhältnis setzen:
(A + B)/K und (C + D)/K
(jeweils mal 100 für Prozentwerte)
Schreib bitte deine Ergebnisse auch hier ins Board.
Schöne Grüße
Uwe |
    
Araiguma (Uwe)

| | Veröffentlicht am Sonntag, den 07. Oktober, 2001 - 13:48: | 
|
 |
|