| Autor |
Beitrag |
    
sara

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 30. April, 2002 - 12:22: | 
|
hallo
Ich möchte unbedingt diese Aufgabe verstehen. Dazu brauche ich wiklich hilfe
Also:
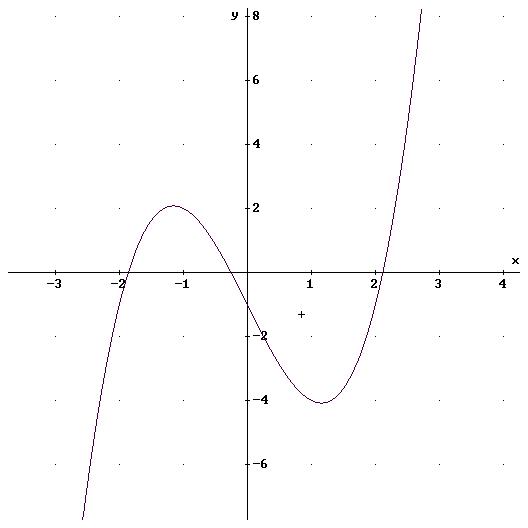
f(x)=x^3-4x-1 Startwert: x0=1
Dazu muss ich die Nullstelle nach Newton berechnen; die Funktion untersuchen, ob es symmetrich ist; die relativen Extremea bestimmen; deren At herausfinden und den Sattelpunkt, fals existiert Berechnen.
Ich habe absolut keine Ahnung wie das funktioniert. Ich verstehe noch nicht einmal dieses ganze Fachchinesisch.
Wenn jemand mir diese Aufgabe Schritt für Schritt erklären könnte, wär ich euch echt dankbar.
Mfg sara |
    
Peter (analysist)

Mitglied
Benutzername: analysist
Nummer des Beitrags: 46
Registriert: 04-2002
| | Veröffentlicht am Dienstag, den 30. April, 2002 - 13:41: | 
|
Hallo sara,
ich hoffe, dass "Fachchinesisch" bezieht sich nur auf das Newtonverfahren, denn dazu braucht es schon einige Termini.
Die Idee des Newtonverfahrens ist eine ganze einfache. Man will die Nullstellen einer Funktion berechnen. Dazu braucht man erst einmal einen Startwert (bei dir x0=1), in dessen Nähe man eine Nullstelle vermutet. Jetzt legt man an dieser Stelle die Tangente an und berechnet deren Nullstelle. Das ist der nächste Startwert. Das wiederholt man solange, bis man der Nullstelle nahe genug gekommen ist. Newton klappt nicht, aber oft!
Fangen wir ganz einfach mal an:
Die Steigung der Tangente in (x0/x0^3-4x0+1) wird mithilfe der Ableitung berechnet: f'(x0)
f'(x)=3x^2-4
m=f'(x0)=3x0^2-4
Tangentengleichung:
y=mx+b
x0^3-4x0+1=(3x0^2-4)x0+b
[allgemein: f(x0)=f'(x0)x0 + b]
x0^3-4x0+1=3x0^3-4x0+b
b=-2x0^2+1
[allgemein: f(x0)-f'(x0)x0= b]
y=(3x0^2-4)x-2x0^2+1
[allgemein: y=f'(x0)x+f(x0)-f'(x0)x0]
Nullstelle der Tangente:
0=(3x0^2-4)x-2x0^2+1
[allgemein: 0=f'(x0)x+f(x0)-f'(x0)x0]
x1=(2x0^2-1)/(3x0^2-4)
[allgemein: x1=(f'(x0)x0-f(x0))/f'(x0)
oder x1=x0-f(x0)/f'(x0)
Mit der allgemeinen Formel geht's einfacher:
f(x)=x^3-4x-1 /// f'(x)=3x^2-4 /// x0=1
x1=1-(-4)/(-1)=-3
x2=-3-(-16)/23=-2.304347826
x3=-1.967489476
x4=-1.869470470
x5=-1.860870682
x6=-1.860805856
x7=-1.860805853
x8=-1.860805853 Hier hat man's dann auf 9 Stellen genau.
Damit ist die Nullstelle hinreichend bestimmt.
Gemeinerweise hat die Funktion noch zwei Nullstellen, die man berechnen kann:
Entweder erneut mit Newton, oder nach erfolgter Polynomdivision durch (x+1.860805853) per p-q-Formel ergibt sich:
x1 = -1.860805853 x2 = 2.114907541 x3 = -0.2541016883
-----------------------------
Symmetrie zum Koordinatensystem ist doch gemeint, oder?
f(x)=f(-x) für alle x => Achsensymmetrie zur y-Achse
-f(x)=f(-x) für alle x => Punktsymmetrie zum Ursprung
Es sind
f(x)=x^3-4x-1
f(-x)=-x^3+4x-1
-f(x)=-x^3+4x+1
f(x) ist im Allgemeinen ungleich f(-x). f(-x) ist im Allgemeinen ungleich -f(x).
=> weder a.s. zur y-Achse noch p.s. zum Ursprung
-----------------------------
Extrema:
Notw. f'(x)=0
Hinr. f'(x)=0 und f''(x)=0
3x^2-4=0
x=+-SQRT(4/3) [SQRT =SQUAREROOT =QUADRATWURZEL]
f''(x)=6x
f''(SQRT(4/3))=6SQRT(4/3)> 0, also Tiefpunkt bei
ca. (1.154700538/-4.079201435)
f''(-SQRT(4/3))=-6SQRT(4/3)<0, also Hochpunkt bei
ca. (-1.154700538/2.079201435)
----------------
Wendepunkte
Sattelpunkte gibt's hier nicht, das sind nämlich Wendepunkt mit der zusätzlichen Eigenschaften, dass die STeigung dort NUll ist.
Notw. f''(x)=0
Hinr. f''(x)=0 und f'''(x)<>0
f''(x)=6x
f'''(x)=6
6x=0
x=0 mögliche Wendestelle
f'''(0)=6 <> 0, also Wendepunkte bei (0/-1)
Gruß
Peter |
|