| Autor |
Beitrag |
    
speedy

| | Veröffentlicht am Sonntag, den 13. Dezember, 1998 - 22:44: | 
|
Wer kann mir einen Tip zur Lösung der Textaufgabe geben?
"Ein Haus hat eine Grundfläche von 108m^2. Die Diagonale beträgt 15m. Wie lang und wie breit ist das Haus?"
Danke,
speedy |
    
Anonym

| | Veröffentlicht am Montag, den 14. Dezember, 1998 - 15:09: | 
|
Hi, stell Dir ein rechtwinkeliges Haus vor, a=Länge des Hauses, b=Breite des Hauses, c = Diagonale der Grundfläche.
Nach Pythagoras und der Flächenformel für Rechtecke ergeben sich folgende beiden Gleichungen:
a^2+b^2=15^2 und a x b = 108
Daraus kannst Du jetzt a und b berechnen. Klar?
Sonst schreib nochmal...
Ciao |
    
Adam Riese

| | Veröffentlicht am Samstag, den 16. Januar, 1999 - 22:55: | 
|
Anonym, Barbara, Karl,
Eure Aufgaben waren unter eine andere bereits gelöste gesetzt worden. Dort sind sie schlecht zu finden, deshalb habe ich in der gleichen Rubrik "Klassen 8-10" --> "Geometrie" diese Aufgaben jeweils als "Neuer Beitrag" aufgemacht. Dies kann ich Euch auch für zukünftige Beiträge empfehlen.
Grüße von Adam. |
    
Anonym

| | Veröffentlicht am Mittwoch, den 26. Mai, 1999 - 18:10: | 
|
hilfe!!!! |
    
Anonym

| | Veröffentlicht am Mittwoch, den 26. Mai, 1999 - 22:42: | 
|
hilfe????? was ist los ???? |
    
Kadmax

| | Veröffentlicht am Donnerstag, den 18. Mai, 2000 - 14:55: | 
|
Hi,
Kann mir eine\r den satz des Pythagoras, in einzelnen Schritten, mit begründung beweisen.
Danke.
Es ist wirklich sehr eilig! |
    
reinhard (Gismo)

| | Veröffentlicht am Donnerstag, den 18. Mai, 2000 - 20:40: | 
|
Hallo Kadmax!
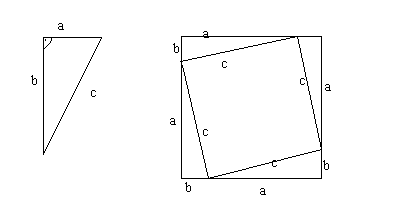
Auf diesem Bild ist links ein rechtwinkeliges Dreieck abgebildet. Die Seiten, die beim rechten Winkel anliegen, heißen Katheten. Und die Seite, die dem rechten Winkel gegenüberliegt, heißt Hypothenuse.
Der Pythagoras sagt folgendes: Die Summe der Quadrate der Katheten ist gleich dem Quadrat der Hypothenuse.
Oder mit den jeweiligen Seitenbezeichnungen:
a²+b²=c²
Wannimmer du also ein rechtwinkeliges Dreieck hast, von dem du 2 Seiten kennst, kannst du mit dem Pythagoras die dazugehörige dritte Seite berechnen.
Beweisen kann man das ganze auch noch. Hierzu habe ich rechts noch eine Zeichnung mitgeschickt.
Das Quadrat hat die Seitenlänge (a+b) und somit eine Fläche von (a+b)²
Man kann es aber auch unterteilen in ein kleineres Quadrat mit Seitenlänge c und 4 rechtwinkeligen Dreiecken mit Kathetenlägen a und b. Mit dieser Unterteilung ergibt sich ein Flächeninhalt von c²+4*(ab/2)=c²+2ab
Da diese beiden Flächeninhalte gleich sind, gilt:
(a+b)²=c²+2ab
a²+2ab+b²=c²+2ab
a²+b²=c²
das war der Beweis.
eine logische Herleitung im üblichen Sinne ist mir nicht bekannt, also habe ich keine Ahnung, wie Pythagoras auf diesen Satz gekommen ist. Aber er stimmt, denn es gibt ja viele verschiedene Beweise.
Reinhard |
    
Kadmax

| | Veröffentlicht am Donnerstag, den 18. Mai, 2000 - 21:43: | 
|
Hi Reinhard,
vielen dank für deine informative und leicht zu verstehende Nachricht.
Kadmax |
    
Bodo

| | Veröffentlicht am Freitag, den 19. Mai, 2000 - 22:04: | 
|
siehe auch hier:
http://www.mathehotline.de/mathe4u/hausaufgaben/messages/24/3143.html
Bodo |
    
MicBac (Senna01)

Neues Mitglied
Benutzername: Senna01
Nummer des Beitrags: 1
Registriert: 03-2002
| | Veröffentlicht am Sonntag, den 03. März, 2002 - 11:38: | 
|
Ein Haus hat eine Grundfläche von 108m^2. Die Diagonale beträgt 15m. Wie lang und wie breit ist das Haus?
Habe zwar die Lösungsidee von anonym gesehen, kann damit aber nichts anfangen!?!
EILT!! |
    
MicBac (Senna01)

Neues Mitglied
Benutzername: Senna01
Nummer des Beitrags: 2
Registriert: 03-2002
| | Veröffentlicht am Sonntag, den 03. März, 2002 - 11:49: | 
|
(Beitrag nachträglich am 03., März. 2002 von senna01 editiert) |
    
Pythagoras oder was

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 03. März, 2002 - 11:52: | 
|
Ein Haus hat eine Grundfläche von 108m^2. Die Diagonale beträgt 15m. Wie lang und wie breit ist das Haus?
Habe zwar die Lösungsidee von anonym gesehen, kann damit aber nichts anfangen!?!
EILT!! |
    
Martin (Martin243)

Junior Mitglied
Benutzername: Martin243
Nummer des Beitrags: 9
Registriert: 02-2001
| | Veröffentlicht am Sonntag, den 03. März, 2002 - 13:46: | 
|
Nennen wir die Länge der Hauswände a und b.
Nach Pythagoras gilt für die Länge der Diagonalen (d=15):
a² + b² = d² = 225
Außerdem wissen wir:
a*b = 108
Wir addieren das Doppelte der zweiten Gleichung zur ersten und erhalten:
a² + b² + 2ab = 225 + 2*108
Also:
a² + 2ab + b² = 441
Nach der 1. Binomischen Formel gilt:
a² + 2ab + b² = (a + b)² = 441
Also:
a + b = Wurzel(441) = 21
Also haben wir:
a + b = 21 und a * b = 108
Wir nehmen an, die Lösung ist ganzzahlig (das wird wohl so sein :-) und zerlegen 108 in seine Primfaktoren:
108 = 2 * 2 * 3 * 3 * 3
Aus diesen Primfaktoren müssen wir zwei Produkte bilden, die die Summe 21 haben (soo viele Möglichkeiten gibt es nicht):
2*2*3 = 12, 3*3 = 9; 9+12 = 21
Also ist a=9 und b=12 (oder umgekehrt), denn Summe (21) und Produkt (108) stimmen! |
|