| Autor |
Beitrag |
    
Lisl (lisl)

Mitglied
Benutzername: lisl
Nummer des Beitrags: 29
Registriert: 02-2001
| | Veröffentlicht am Dienstag, den 21. Januar, 2003 - 09:30: | 
|
Hallo, ich habe eine Funktion, die lautet f(x)=(1)/(x²+x)² und bräuchte hierzu die Stammfunktion zum weiteren Rechnen. Kann mir da jemand weiterhelfen? Und wenn möglich bitte auch kurz den Lösungsweg angeben, damit ich das selber irgendwie nachvollziehen kann für weitere Aufgaben.
Danke schon mal
|
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 266
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 21. Januar, 2003 - 14:17: | 
|
VIELLEICHT KANN EIN ANDERER NOCH HELFEN,
denn das ergebniss ist:
F(x)=-[(1/x)+(1/(x+1))+2*ln(x)-2*ln(x+1)]
und ich weiß das man das mit Partialbruchzerlegung berechnet, aber irgendwie finde ich den ansatz hier nicht!
mfg |
    
Lisl (lisl)

Mitglied
Benutzername: lisl
Nummer des Beitrags: 30
Registriert: 02-2001
| | Veröffentlicht am Dienstag, den 21. Januar, 2003 - 18:05: | 
|
Okay danke, das macht nix. Ich hoffe sowieso das nach sowas in der Prüfung nicht gefragt wird.... Für die Exponentialfkt. hab ich das ja mittlerweile begriffen!!! |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 875
Registriert: 02-2002
| | Veröffentlicht am Dienstag, den 21. Januar, 2003 - 18:11: | 
|
1/[x²(x+1)²] = A/x + B/x² + C/(x+1) + D/(x+1)²
= [A*x*(x+1)² + B*(1+x)² + C*x²*(x+1) + D*x²] / ()
| | | x³: | A | | +C | | = 0 | | x²: | 2A | +B | +C | +D | = 0 | | x¹: | A | +2B | | | = 0 | | x°: | | B | | | = 1 | | x¹: | A | | | | =-2 | | x³: | | | C | | = 2 | | x²: | | | | D | =-1 |
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Niels (niels2)

Erfahrenes Mitglied
Benutzername: niels2
Nummer des Beitrags: 290
Registriert: 06-2001
| | Veröffentlicht am Dienstag, den 21. Januar, 2003 - 21:28: | 
|
Ich hoffe, man kann mein geschmiere noch lesen...
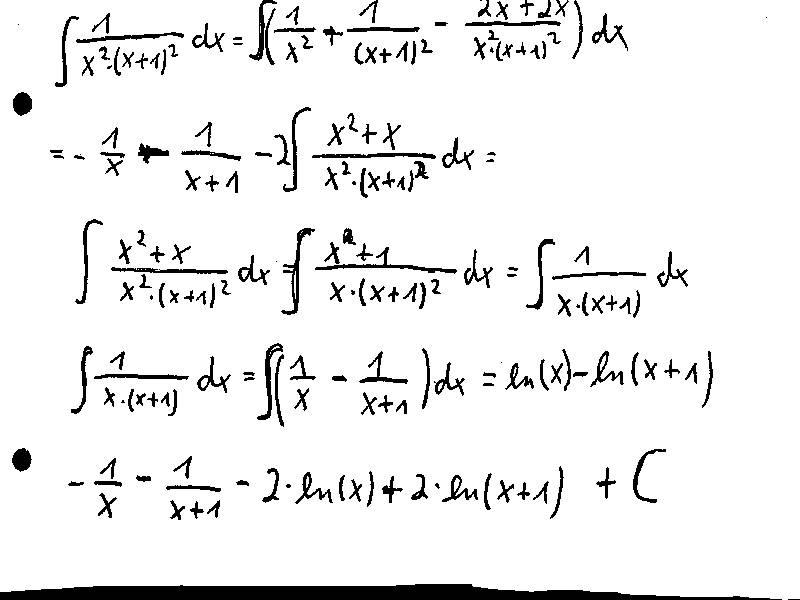
ein wirklich putziges Integral...
Gruß N. |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 270
Registriert: 10-2002
| | Veröffentlicht am Dienstag, den 21. Januar, 2003 - 21:36: | 
|
Meinen herzlichsten Dank an Friedrich und Niels! Manchmal hat man halt ein Brett vor dem Kopf, oder einen dicken Kopf vom Abend davor ;-)
mfg |