| Autor |
Beitrag |
    
Nadine (mermaid)

Neues Mitglied
Benutzername: mermaid
Nummer des Beitrags: 1
Registriert: 11-2002
| | Veröffentlicht am Samstag, den 16. November, 2002 - 10:12: | 
|
Hi!
Ich habe ein Riesenproblem mit (meiner Meinung nach doch eigentlich gar nicht so komplizierten) Gleichungen dieser Art:
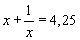
Wäre wirklich riesig nett, wenn mir da jemand weiterhelfen könnte...
Ciao, Nadine |
    
Ferdi Hoppen (tl198)

Erfahrenes Mitglied
Benutzername: tl198
Nummer des Beitrags: 127
Registriert: 10-2002
| | Veröffentlicht am Samstag, den 16. November, 2002 - 10:35: | 
|
mit x durchmultiplizieren, du erhälst:
x^2+1=4,25x
x^2-4,25x+1=0
Quadratische Gleicung lösen, bringet
x=4 oder x=0,25 als lösungen.
mfg
tl198 |
    
Josef Filipiak (filipiak)

Erfahrenes Mitglied
Benutzername: filipiak
Nummer des Beitrags: 198
Registriert: 10-2001
| | Veröffentlicht am Samstag, den 16. November, 2002 - 10:39: | 
|
Hallo Nadine,
x + 1/x = 4,25 | Hauptnenner ist x
x²+1 = 4,25x | quadratische Gleichung
x²-4,25x+1 = 0
x1;2=4,25/2±Ö(4,25/2)² -1
x1;2=4,25/2±Ö18,0625/4 -4
x1;2=4,25/2±Ö14,0625/4
x1=4,25/2 + 3,75/2 = 4
x2=4,25/2 - 3,75/2 = 0,5/2 = 0,25
Gruß Filipiak |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 668
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 16. November, 2002 - 10:41: | 
|
mit x mult., rechts nach links
x² - 4,25x + 1 = 0
x = 2,125 ±Wurzel(2,125²-1)
Wenn das Erlernen der Mathematik einigermasßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Nadine (mermaid)

Neues Mitglied
Benutzername: mermaid
Nummer des Beitrags: 2
Registriert: 11-2002
| | Veröffentlicht am Sonntag, den 17. November, 2002 - 09:09: | 
|
Sorry, aber quadratische Gleichungen kommen bei uns wahrscheinlich erst Ende dieses Schuljahres dran, sonst hätte ich die Aufgabe vielleicht auch selbst lösen können... Aber gibt es keine andere Möglichkeit? Am besten ich nehm' noch mal eine Aufgabe dieser Art von ganz Anfang an (wenn jemand Fehler entdeckt, bitte unbedingt melden!):
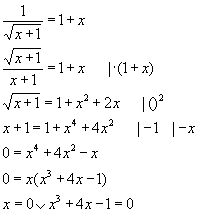
Ok, so weit komm' ich ja noch, aber wie geht's dann weiter, also wie kann ich diese Gleichung nach x auflösen:
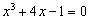
Wäre mal wieder riesig nett, wenn ich ein bißchen Hilfe bekommen würde...
 Ciao, Nadine Ciao, Nadine
|
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 677
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 17. November, 2002 - 17:28: | 
|
da siehst Du es (ist auch mathdraw, aber direkt)
(ignorier die überfüssigen +Zeichen einfach)
Wenn das Erlernen der Mathematik einigermasßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 678
Registriert: 02-2002
| | Veröffentlicht am Montag, den 18. November, 2002 - 07:36: | 
|
sollte nur ein Test sein, Sendevorgan ließ sich aber nicht abbrechen.
(Beitrag nachträglich am 18., November. 2002 von friedrichlaher editiert)
Wenn das Erlernen der Mathematik einigermasßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
|