| Autor |
Beitrag |
    
Nancy Seidemann (Anomi)

| | Veröffentlicht am Sonntag, den 22. April, 2001 - 10:39: | 
|
gegeben ist dieses Bild:
/ S\
/ / \ \
/ / \ \
D ----/-----\---C
!* / \ *!
! / \ !
!/ \!
/_____________\
A a B
*= hD und hc(die Höhen von D und C)
Das Fünfeck in meinem Bild besteht aus einem Quadrat und einem gleichseitigen Dreieck mit der Seite a.Berechne den Abstand der Punkte A und S sowie den Abstand des Punktes D von AS.
Die Lösungen besitze ich bereits...könnt ihr mir bei den rechenweg helfen?
also beim erts3en teil kommt AS=a* die wurzel aus 2+ wurzel aus 3 raus.
und beim zweiten teil: a/2 . die wurzel aus 2- die wurzel aus 3 raus.
DANKE! |
    
Zorro

| | Veröffentlicht am Sonntag, den 22. April, 2001 - 14:52: | 
|
Hi Nancy,
unter großem detektivischen Einsatz ist es mir tatsächlich gelungen, Deine Aufgabenstellung und Deine Lösungen nachzuvollziehen. *g*
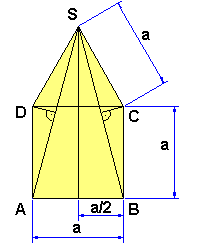
Aufgabe 1:
Lösung mit Pythagoras:
AS² = (a/2)² + [a + a*sin(60°)]²
AS² = a²/4 + [a (1+Ö(3/4)]²
AS² = a²/4 + a²[1+Ö(3/4)]²
AS² = a² (1/4 + 1 + Ö(3) + 3/4)
AS² = a² (2 + Ö(3))
AS = a * Ö[2 + Ö(3)] ... hier hättest Du in Deiner Lösung ruhig Klammern angeben können.
Aufgabe 2:
Lösung mit Pythagoras:
hD² = a² - (AS/2)²
hD² = a² - [a/2 Ö(2 + Ö(3))]²
hD² = a² - (a²/4)(2 + Ö(3))
hD² = a²/4 [4 –2 -Ö(3)]
hD² = a²/4 [2 - Ö(3)]
hD = a/2 Ö[2 - Ö(3)]
Gruß, Zorro |
|