| Autor |
Beitrag |
    
daniel

| | Veröffentlicht am Dienstag, den 13. März, 2001 - 19:59: | 
|
kann mir irgendjemand ganz fix eine Stammfunktion zu f: f(x)=ln(5x/((x^2)+4)) angeben?
(wäre noch die Rechnung bzw. Erläuterung dabei, so könnte ich mein Glück ja kaum fassen...) |
    
OliverKnieps (Oliverk)

| | Veröffentlicht am Dienstag, den 13. März, 2001 - 20:44: | 
|
Hi Daniel,
wir machen es uns (zunächst) ganz einfach und wenden auf
f(x) einfach die 2. Logarithmenregel an, also
log ( a / b ) = log a - log b
und für f(x) bedeutet das:
f(x) = ln (5x) - ln (x2 + 4)
Den ersten Summanden, ln(5x) kannst du sicherlich schnell integrieren. Mit ln (x2 + 4) müssen wir uns aber etwas ausführlicher befassen:
Zunächst integrieren wir partiell, und zwar beginnen wir mit einem Trick: Wir integrieren die 1 vor ln (x2 + 4). Warum, wirst du sicherlich im Verlauf schnell sehen! Also
Int = Integralzeichen
int ln(x2 + 4) dx = [ x * ln(x2 + 4)] - int (2x2)/(x2 + 4) dx
Soweit so gut. Das Restintegral lösen wir duch Polynomdivision, da der Bruch unecht gebrochen ist, also findest du
(2x2) : (x2 + 4) = 2 + (-8/(x2 + 4))
Auch die "2" läßt sich leicht integrieren und schließlich kommen wir zum Schluß unseres gar nicht einfachen Integrals: Die Integration des bei der Polynomdivision enstandenen Restes, also
(-8/(x2 + 4)) ergibt eine Arcustangensfunktion. Ich weiß nicht, ob Du das schon gehabt hast, aber wenn der Lehrer Euch das so aufgegeben hat....:
Die - 8 soll uns im Moment nicht interessieren und schreiben sie vor das Integral. Nehmen wir uns die "normale" Arcustangensfunktion, speziell ihre Ableitung vor, so gilt
g(x) = Arctan(x)
g'(x)= 1/(x2 + 1)
Man erkennt also schon die Ähnlichkeit. Um die letzte Hürde -8 * Int (1/(x2 + 4) dx zu nehmen, substituieren wir x = 2u, also gilt
dx = 2 du, und eingesetzt finden wir
-8 Int 1/(4u2 + 4) du
Ausklammern von 4, kürzen mit -8 gibt
-2 Int 1/(u2 + 1) du, also dann endlich (!)
-2 [ Arctan (u) + C] (C = Konstante)
Durch Rücksubstitution ergibt sich:
-2 [Arctan (x/2) + C]
So, das war es zum Glück schon. Und weil Du Dein Glück kaum fassen sollst, wage ich mich mal daran, alle Teilintegrale zusammenzufassen, also los gehts:
F(x) = (1/5)*( (5x)ln(5x)- 5x ) + 2x - 2 * Arctan(x/2) + C'
Falls Du Fragen hast, dann schreib doch einfach hier ins Forum oder an meine email!
Viele Grüße
 Oliver Oliver |
    
OliverKnieps (Oliverk)

| | Veröffentlicht am Dienstag, den 13. März, 2001 - 20:49: | 
|
Ups, das kommt davon, wenn man nebenbei noch Musik von TOTO hört, wegen dem Minuszeichen bei
f(x) = ln (5x) - ln (x2 + 4)
heisst es zum Schluss richtig:
F(x) = = (1/5)*( (5x)ln(5x)- 5x ) - 2x + 2 Arctan (x/2) + C'.
Sorry!
 Oliver Oliver |
    
Fern

| | Veröffentlicht am Mittwoch, den 14. März, 2001 - 07:13: | 
|
Hallo Oliver und Daniel,
Kleiner Fehler:
Endresultat ist: xln(x²+4) - 2x + 4arctan(x/2)
===========================
Der Fehler liegt bei der Substitution von u = x/2
Gruß, Fern |
    
Fern

| | Veröffentlicht am Mittwoch, den 14. März, 2001 - 07:24: | 
|
Ups,
Jetzt habe ich selbst allerlei durcheinandergebracht:
Endresultat:
xln(5) + xln[x/(x²+4)] + x - 4*arctan(x/2)
=================================== |
    
Fern

| | Veröffentlicht am Mittwoch, den 14. März, 2001 - 09:05: | 
|
Hallo Daniel,
Ich habe nochmal alles ausführlicher aufgeschrieben. Oliver hat auch noch bei der Zusammenfassung einige Terme verloren.
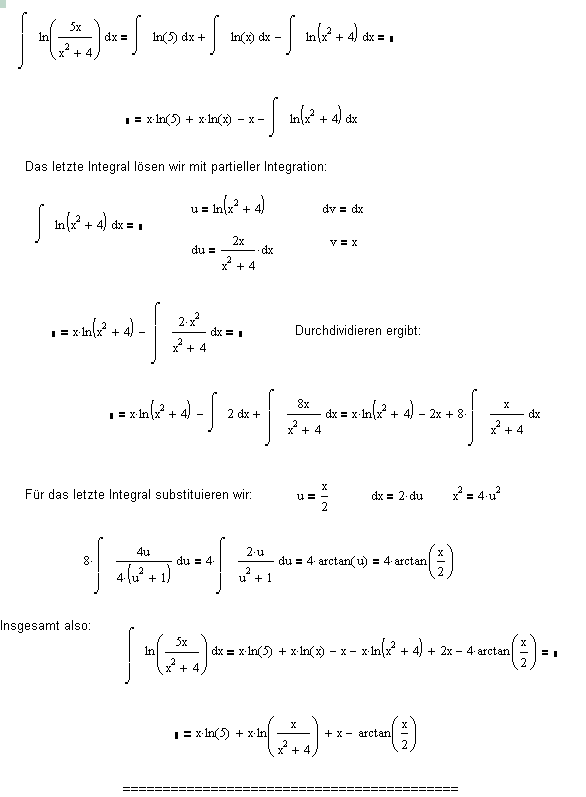 |
    
Fern

| | Veröffentlicht am Mittwoch, den 14. März, 2001 - 09:10: | 
|
Es scheint fast unmöglich zu sein, dies richtig hinzubringen:
Zum Schluss natürlich: -4*arctan(x/2)
============================== |
    
H.R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 14. März, 2001 - 14:55: | 
|
Hallo Fern,
Als Trost:
Der Grund für Dein Ungemach könnte darin liegen,
dass für Dich ein wichtiger Count-down beginnt !
Es gilt nämlich
1000 - 979 = 21 > 20 > 19 ....usw.
Mit freundlichen Grüssen
H.R.Moser,megamath. |
    
OliverKnieps (Oliverk)

| | Veröffentlicht am Mittwoch, den 14. März, 2001 - 15:07: | 
|
Hallo Fern, H.R. Moser,
vielleicht hätte ich mir doch die Mühe machen sollen, das Integral auf dem Papier vorzurechnen, naja, sollte schnell gehen und wollte noch TV Total sehen....sorry!
Jetzt muss ich allerdings gestehen, Fern, das ich bei deinem Rest (Polynomdivision), und seiner Integration etwas durcheinanderkomme, aber ich gehe mal davon aus, dass es nicht (8x)/(x2+4) heißt, sondern nur (8)/(x2+4), oder? Zumindest würde dann ja die Substitution und die Stammfunktion Sinn machen....
Außerdem ist meine Substitution doch auch dieselbe wie bei Dir, warum liegt dann da Deiner Meinung nach der Fehler?
Viele Grüße
 Oliver Oliver |
    
Fern

| | Veröffentlicht am Mittwoch, den 14. März, 2001 - 17:53: | 
|
Hallo Oliver,
Du hast Recht: nach der Polynomdivision ergibt sich kein x im Zähler!
Ich hatte die richtige Lösung auf dem Papier, habe dann aber beim Abtippen auf dem Schirm (falsch) weitergerechnet und dann wieder die (richtige) Lösung vom Papier abgeschrieben.
Bei deiner Substitution hast du einen Faktor 2 verloren: dx = 2du.

Diese Methode nennt man sukzessive Irrtumselimination
Gruß, Fern |
    
Rainer

| | Veröffentlicht am Donnerstag, den 15. März, 2001 - 00:19: | 
|
Wie gehts Daniel eigentlich ?! |
|