| Autor |
Beitrag |
    
Nadja

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 10. Oktober, 2002 - 16:19: | 
|
gegeben eine parabel 3. ordnung die zum urpsrung symmetrisch sind und durch den punkt p(3/0) gehen
a, bestimme die gleichung derjenigen parabel k1 der schar die durch s(5/5) geht. Ermittle hoch und tiefpunkte und die steigung der wendetangente von k1!
b,
ermittle unter den parabeln negativer steigung diejenige die mit der winkelhalbierende des 1. quadranten eine fläche kleinsten inhalts einschliesst..wie gross ist der inhalt ?
c, jede parabel der schar neg. steigung im ursprung schneidet die winkelhalbierende des 1. quad. im punkt mit dem x wert s.
für welches s ist der inhalt der fläche im 4. quad. zwischen parabel und der x achse ebnso gross wie der inahlt der von der parabel, der x achse und der geraden x=s begrenzten fläche ?
d, berechne die steigung der ursprungsgeraden welche die fläche von teilaufgabe b) halbiert
BITTE BITTE BITTE...das muss ganz schnell gehen...einzelne teilaufgaben würden mir schon sehr helfen...
danke :-)
Nadja |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 557
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 10. Oktober, 2002 - 22:38: | 
|
wenn sie symetrisch zum Ursprung ist, darf sie nur x³ und x enthalten,
also
f(x) = ax³+bx
p(3/0):
f(3)=0: 27a + 3b = 0; b = -9a
-----------------------------
a)
f(5)=5: 125a+ 5b = 5
135a+15b = 0
375a+15b = 15; 240a = 15; a = 16
16*27 = -3b; b = -144; f(x) = 16x³-144x
---------------
b)
f'(x) = 3ax²+b;
damit
die Steigung immer negativ ist muß a<0, b<0 gelten,
DAS IST UNMÖGLICH WEGEN b = -9a .
( es
ist wohl, wie für c, negative Steigung IM URSPRUNG
gemeint, es genügt also b < 0
)
Die
Winkelhalbierende des 1ten Quadranten ist y=x
und
soll, damit eine Fläche gebildet wird, diese 2mal schneiden
Der
eine Schnittpunkt ist bereit gegeben: x=0, y=0
ax³+bx = x; ax²+b=1;
x = ±Wurzel( (1-b)/a ) sin der 2. und 3. Schnitt.
Das
ergibt 2 Flächenstücke 2*F, die der Symetrie wegen aber gleichglächig sind.
um
das Extremum zu finden ist also
g(x) = (ax³+bx) - x von 0 bis Wurzel( (1-b)/a ) zu integrieren
und
das von a,b abhängige Extremum zu bestimmen;
G(x) = Integral( g(x) ) = ax^4/4 + (b-1)x²/2
von 0 bis Wurzel( (1-b)/a ) : F = G( Wurzel( (1-b)/a ) - G(0)
F = F(a,b) = a*[(1-b)/a]²/4 + (b-1)*[(1-b)/a]/2 - 0
F(a,b) = (1-b)²/(4a) - (1-b)²/(2a)
nun
für b = -9a ( aus der Bedingung p(3/0) ) einsetzen
4F(a) = -2(1+9a)²/a und nach a ableiten
[4F(a)]' = -2[2*(1+9a)*a - (1+9a)*1]/a²
für
das Extremum muß der Zähler 0 werden
2*(1+9a)*a - (1+9a) = 0;
Etweder
a = 1/2, b = -9/2
oder
1+9a = 0, a = -1/9, b = 1 aber dafür ist f'(0) = 1 > 0
| 4F(+1/2) | = 2*(1+9/2)²*2; | F | = (11/2)²
(oder das doppelte wenn beide Stücke gemeint sind
)
c,d) Morgen, wenn noch von interesse
|
    
mythos2002 (mythos2002)

Erfahrenes Mitglied
Benutzername: mythos2002
Nummer des Beitrags: 151
Registriert: 03-2002
| | Veröffentlicht am Donnerstag, den 10. Oktober, 2002 - 22:47: | 
|
Hi,
mal zum Anfang:
die zum Ursprung symmetrische kubische Parabel muss die Gleichung
y = ax³ + bx haben (nur ungerade Potenzen bei ungerader Funktion)
Die zum Ursprung symmetrische Funktion nennt man auch ungerade Funktion, und es gilt f(-x) = -f(x). Daher können in dieser nur ungerade Potenzen vorkommen.
Für a und b können wir mittels des gegebenen Punktes P(3|0) eine Beziehung aufstellen, indem wir diesen in die Parabelgleichung einsetzen:
0 = 27a + 3b --> b = -9a, das wieder n die Parabegleichung einsetzen:
y = ax³ - 9ax
Dies ist die Gleichung einer Kurvenschar, die durch Variation des Parameters a erzeugt wird.
a) Eine Kurve dieser Schar soll durch S(5|5) gehen, also setzen wir den Punkt wieder in die Kurvengleichung ein:
y = ax³ - 9ax
5 = 125a - 45a
80a = 5
a = 1/16
Die Kurve heisst dann: y = (1/16)x³ - (9/16)x.
Die Diskussion der Kurve geht nun wie gewohnt.
b) c) d) schauen nach "Arbeit" aus, zu dieser Tageszeit aber nimmer ....
Tipp: Mach dir eine gute Handskizze bzw. lasse dir die Kurven mal für verschiedene a plotten (zeichnen) - das kannst mit einem Programm am PC machen oder auch online im Netz, dann siehst du schon sehr viel ....
Gr
mYthos |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 559
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 11. Oktober, 2002 - 11:56: | 
|
mYthos Weg, f(x)
sofort
als f(x) = ax³-9ax = a*(x³-9x)
zu
bestimmen ist natürlich eleganter und macht es einfacher.
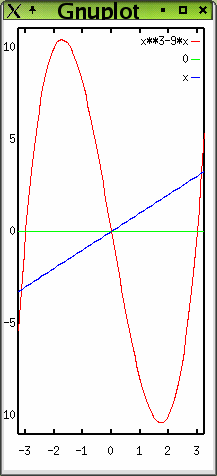
c)
Das Bild ist für a=1, die Schnittpunkte, x=s, sind,
wie
schon für (b), ±Wurzel( (1 - 9a)/a ), hier also ±Wurzel( 10 ),
aber
im 4ten Quadranten begrenzen f(x) und die xAchse keine Fläche(und das bleibt so für beliebige a>0).
Was
ist also wirklich gefragt?
(Beitrag nachträglich am 11., Oktober. 2002 von friedrichlaher editiert) |
    
Q.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 11. Oktober, 2002 - 13:39: | 
|
Hallo Friedrich,
kleiner Vorzeichenfehler: s = +-Wurzel((1 + 9a)/a)
Bei c) ist wohl folgendes gemeint (gelbe Fläche = blaue Fläche):
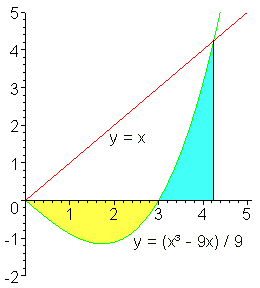
mit der Lösung a = 1/9
|
    
Q.

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 11. Oktober, 2002 - 17:06: | 
|
Hallo nochmal,
leider haben sich bei der Lösung zu b) einige Rechenfehler eingeschlichen (ich verwende Friedrichs Bezeichnungen):
Die Winkelhalbierende y = x liegt für 0<x<s oberhalb der Parabel, daher
g(x) = Integral( x - (ax³+bx) ) von 0 bis Wurzel((1-b)/a)
Der Faktor 2 bei "4F(a)" ist nicht richtig (und kein negatives Vorzeichen), daher
4F(a) = (1+9a)²/a
Bei der Ableitung sollte man die Quotientenregel in folgender Form anwenden:
[4F(a)]' = [2*(1+9a)*9*a - (1+9a)²*1]/a² = (81*a² - 1)/a²
daher Extrema für a = +- 1/9 , Minimum für a = 1/9 und y = (x³ - 9x)/9
Fmin = 9 (oder das Doppelte wenn beide Stücke gemeint sind)
|
|