| Autor |
Beitrag |
    
Jule

| | Veröffentlicht am Montag, den 22. Januar, 2001 - 15:51: | 
|
Könnt Ihr mir bitte helfen, weiß nicht wie ich diese Aufgabe lösen soll:
Welche Parabeln P: y=ax²+c schneiden die Kurve K: y=ln x orthogonal? Für welche dieser Parabeln liegt der Schnittpunkt mit K auf der x - Achse?
Wäre echt schön,wenn noch heute jemand Zeit für mich hätte. Danke schon einmal im Voraus für Eure Mühe!!! |
    
Frank (Norg)

| | Veröffentlicht am Dienstag, den 23. Januar, 2001 - 10:43: | 
|
Orthogonal bedeutet für Steigungen m1=-1/m2.
Du hast zwei Funktionen:
f(x) = ax2+c, f'(x) = 2ax
g(x) = ln x, g'(x) = 1/x.
Es muß gelten:
I f(x) = g(x)
II f'(x) = -1/g(x)
II 2ax = -1/(1/x)
2ax = -x
ax = -1/2*x
Mit x¹0 also:
a = -1/2
I ax2 + c = ln x
-1/2x2 + c = lnx
c=x/2+lnx
Diese Gleichung läßt sich nicht weiter vereinfachen, mit x wählst du den Schnittpunkt aus.
Soll er auf der x-Achse liegen, so muß er also eine Nullstelle beide Funktionen sein, da der ln
nur eine Nullstelle bei x=1 hat, gilt für diesen Fall:
c=1/2.
MfG Frank.
PS.:
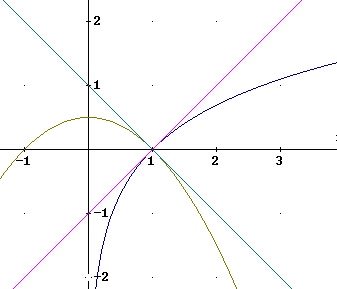 |
    
Jule

| | Veröffentlicht am Dienstag, den 23. Januar, 2001 - 21:09: | 
|
Vielen Dank Frank, Du warst mir eine große
Hilfe! Ihr seid echt klasse!!!!!!!!!
Liebe Grüße Jule! |
    
Frank (Norg)

| | Veröffentlicht am Mittwoch, den 24. Januar, 2001 - 11:15: | 
|
Ich fühle mich geschmeichelt.
MfG Frank. |
|